题目内容
19.小吃部内一小型餐桌,桌面的长为120cm,宽为80cm,桌布的长为180cm,宽为120cm,将桌布按与桌面长宽相间的方向铺在桌面上,使桌面相对两边桌布下垂的宽度各自相等,求此时桌布四个角下垂的大致尺寸(保留根号)分析 由勾股定理分别求出桌面和桌布的对角线长,即可得出结果.
解答 解:由勾股定理得:$\sqrt{12{0}^{2}+8{0}^{2}}$=40$\sqrt{13}$,$\sqrt{18{0}^{2}+12{0}^{2}}$=60$\sqrt{13}$,
∴桌布四个角下垂的大致尺寸为$\frac{1}{2}$(60$\sqrt{13}$-40$\sqrt{13}$)=10$\sqrt{13}$(cm);
答:此时桌布四个角下垂的大致尺寸为10$\sqrt{13}$cm.
点评 本题考查了矩形的性质、勾股定理的应用;熟练掌握勾股定理是解决问题的关键.

练习册系列答案
相关题目
2.方程组$\left\{\begin{array}{l}{x+y=1}\\{2x+y=5}\end{array}\right.$的解为( )
| A. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-2}\\{y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=4}\\{y=-3}\end{array}\right.$ |
 已知函数y=x+$\frac{1}{x}$(x>0)的图象如图所示,其中当x=1时,函数取得最小值2,请结合图象,解答以下问题:
已知函数y=x+$\frac{1}{x}$(x>0)的图象如图所示,其中当x=1时,函数取得最小值2,请结合图象,解答以下问题: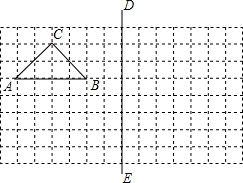 如图,在所给网络图(每小格均为边长是1的正方形)中完成下列各题:
如图,在所给网络图(每小格均为边长是1的正方形)中完成下列各题: 如图,矩形ABCD中,AB=4,BC=6,对角线AC,BD交于点O,延长DC到E,连接OE,交BC于点F.若CE=2,试求CF的长.
如图,矩形ABCD中,AB=4,BC=6,对角线AC,BD交于点O,延长DC到E,连接OE,交BC于点F.若CE=2,试求CF的长.