题目内容
20.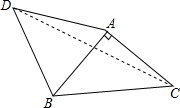 已知:如图,等腰直角△ABC,∠BAC=90°,AB=AC,点D为△ABC外一点,∠ADB=45°,连接CD,AD=4$\sqrt{2}$,CD=10,则AC=2$\sqrt{5}$.
已知:如图,等腰直角△ABC,∠BAC=90°,AB=AC,点D为△ABC外一点,∠ADB=45°,连接CD,AD=4$\sqrt{2}$,CD=10,则AC=2$\sqrt{5}$.
分析 过B作BE⊥AD于E,过C作CF⊥AD交DA的延长线于F,由∠BAC=90°,AB=AC,得到∠EAB+∠FAC=∠EAB+∠EBA=90°,证出∠ABE=∠FAC,推出△ABE≌△AFC,得到AE=CF,BE=AF,设AE=CF=x,AF=BE=DE=y,根据勾股定理得到CF=AE=$\sqrt{2}$,AF=BE=DE=3$\sqrt{2}$,AC=$\sqrt{A{F}^{2}+C{F}^{2}}$=2$\sqrt{5}$.
解答 解:如图,过B作BE⊥AD于E,过C作CF⊥AD交DA的延长线于F,
∵∠BAC=90°,AB=AC,
∴∠EAB+∠FAC=∠EAB+∠EBA=90°,
∴∠ABE=∠FAC,
在△ABE与△CAF中,
$\left\{\begin{array}{l}{∠ABE=∠CAF}\\{AB=AC}\\{∠AEB=∠F=90°}\end{array}\right.$,
∴△ABE≌△AFC,
∴AE=CF,BE=AF,
∵∠ADB=45°,
∴DE=BE,
设AE=CF=x,AF=BE=DE=y,
在Rt△CDF中,DF2+CF2=CD2,
即:(x+2y)2+x2=102,
∵x+y=4$\sqrt{2}$,
∴x=$\sqrt{2}$,y=3$\sqrt{2}$,
∴CF=AE=$\sqrt{2}$,AF=BE=DE=3$\sqrt{2}$,
∴AC=$\sqrt{A{F}^{2}+C{F}^{2}}$=2$\sqrt{5}$.
故答案为:2$\sqrt{5}$.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,三角形的面积的求法,正确的作出辅助线构造全等三角形是解题的关键.

练习册系列答案
相关题目
10. 如图所示,AB,CD,EF交于点O,∠1=20°,∠BOC=80°,求∠2的度数( )
如图所示,AB,CD,EF交于点O,∠1=20°,∠BOC=80°,求∠2的度数( )
 如图所示,AB,CD,EF交于点O,∠1=20°,∠BOC=80°,求∠2的度数( )
如图所示,AB,CD,EF交于点O,∠1=20°,∠BOC=80°,求∠2的度数( )| A. | 60° | B. | 70° | C. | 80° | D. | 100° |
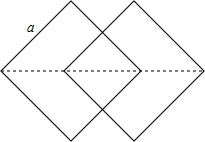 如图,这是由一个边长为a的正方形沿一条对角线的方向平移$\frac{\sqrt{2}a}{2}$得到的图案.
如图,这是由一个边长为a的正方形沿一条对角线的方向平移$\frac{\sqrt{2}a}{2}$得到的图案. 如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(-1,0),另一个交点为B,且与y轴交于点C.
如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(-1,0),另一个交点为B,且与y轴交于点C. 如图,∠AOB=35°,∠BOC=90°,OD是∠AOC的平分线,求∠BOD的度数.
如图,∠AOB=35°,∠BOC=90°,OD是∠AOC的平分线,求∠BOD的度数.