题目内容
5．阅读下文，寻找规律．计算：（1-x）（1+x）=1-x2，（1-x）（1+x+x2）=1-x3，（1-x）（1+x+x2+x3）=1-x4…．
（1）观察上式，并猜想：（1-x）（1+x+x2+…+xn）=1-xn+1．
（2）根据你的猜想，计算：1+3+32+33…+3n=-$\frac{1}{2}（1-{3^{n+1}}）$．（其中n是正整数）
分析 （1）归纳总结得到一般性规律，写出即可；
（2）原式变形后，利用得出的规律计算即可得到结果．
解答 解：解：（1）（1-x）（1+x+x2+…+xn）=1-xn+1；
（2）1+3+32+…+3n=-$\frac{1}{2}$（1-3）（1+3+32+33…+3n）=-$\frac{1}{2}（1-{3^{n+1}}）$．
故答案为：（1）1-xn+1，
（2）-$\frac{1}{2}（1-{3^{n+1}}）$．
点评 本题考查了平方差公式，解决本题本题的关键是熟记平方差公式．
练习册系列答案
相关题目
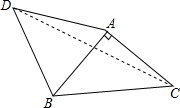已知：如图，等腰直角△ABC，∠BAC=90°，AB=AC，点D为△ABC外一点，∠ADB=45°，连接CD，AD=4$\sqrt{2}$，CD=10，则AC=2$\sqrt{5}$．
如图，在Rt△ABC中，∠C=90°，∠BAC的平分线AD交BC边于点D，以AB上一点O为圆心作⊙O，使⊙O经过点A和点D．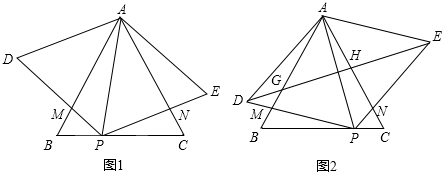
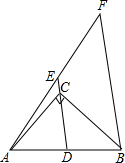如图，∠ACB=90°，D为AB的中点，连接DC并延长到E，使CE=$\frac{1}{3}$CD，过点B作BF∥DE，与AE的延长线交于点F．若AB=6，则BF的长为8．