题目内容
15. 如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(-1,0),另一个交点为B,且与y轴交于点C.
如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(-1,0),另一个交点为B,且与y轴交于点C.(1)求m的值,求点B的坐标;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)该二次函数图象上是否有一点Q(x,y)使S△ABQ=S△ABC,求点Q的坐标.
分析 (1)由二次函数y=-x2+2x+m的图象与x轴的一个交点为A(-1,0),利用待定系数法将点A的坐标代入函数解析式即可求得m的值;根据求得二次函数的解析式,然后将y=0代入函数解析式,即可求得点B的坐标;
(2)根据函数解析式求得对称轴,由二次函数图象上有一点P,又由PA+PC的值最小,连接CB交对称轴于点P,求得BC的解析式即可求得点P的坐标.
(3)根据函数解析式求得点C的坐标,由二次函数图象上有一点Q(x,y),又由S△ABQ=S△ABC,可知点Q与点C的纵坐标的绝对值相等,代入函数的解析式即可求得点Q的坐标.
解答 解:(1)∵二次函数y=-x2+2x+m的图象与x轴的一个交点为A(-1,0),
∴将点B(-1,0)代入y=-x2+2x+m中,得:
-1-2+m=0,
解得:m=3;
∵二次函数的解析式为:y=-x2+2x+3,
∴当y=0时,-x2+2x+3=0,
解得:x=3或x=-1,
∴B(-1,0);
(2)设直线BC的解析式为:y=kx+b,有:
$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$,
故直线BC:y=-x+3;
抛物线y=-x2+2x+3的对称轴为x=1,
连接BC交对称轴于点P,如图,
设点P坐标(1,t),
把(1,t)代入y=-x+3得t=2,
故点P坐标为P(1,2);
(3)∵当x=0时,y=3,
∴C(0,3),
∵设二次函数图象上有一点Q(x,y)使S△ABQ=S△ABC,
∴AB•|yQ|=AB•|yC|,
∴|yQ|=|yC|,
∵yC=3,
∴|yQ|=3,
∴yQ=±3,
∴当y=3时,-x2+2x+3=3,
解得:x=0或x=2,
∴点Q的坐标为(2,3).
∴当y=-3时,-x2+2x+3=-3,
解得:x=1+$\sqrt{7}$或x=1-$\sqrt{7}$,
∴点Q的坐标为(1+$\sqrt{7}$,-3)或(1-$\sqrt{7}$,-3).
综上所述,Q点坐标为Q1(2,3),Q2(1+$\sqrt{7}$,-3),Q3(1-$\sqrt{7}$,-3).
点评 本题考查了待定系数法求二次函数的解析式,考查了一元二次方程的解法以及三角形的面积问题等知识.此题综合性较强,但难度不大,属于中档题,解题的关键是掌握二次函数与一元二次方程的关系,注意数形结合与方程思想的应用.

 一个正方体的平面展开图如图所示,将它折成正方体后,“主”字的对面的字是( )
一个正方体的平面展开图如图所示,将它折成正方体后,“主”字的对面的字是( )| A. | 富 | B. | 强 | C. | 自 | D. | 由 |
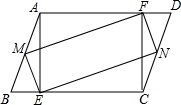 如图,?ABCD中,AE⊥BE于E,CF⊥AD于F,M、N分别为AB、CD的中点.求证:四边形MENF是平行四边形.
如图,?ABCD中,AE⊥BE于E,CF⊥AD于F,M、N分别为AB、CD的中点.求证:四边形MENF是平行四边形. 如图,△ABC内接于⊙O,弧AB=弧AC,D是弧BC上任意一点,AD=6,BD=5,CD=3,求DE的长.
如图,△ABC内接于⊙O,弧AB=弧AC,D是弧BC上任意一点,AD=6,BD=5,CD=3,求DE的长.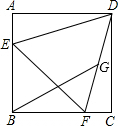 如图,边长为4的正三角形DEF与正方形ABCD共有一顶点D,点E、F分别在线段AB、BC上,将点B与线段DF的中点G连接,则线段BG的长是$\sqrt{6}$+$\sqrt{2}$.
如图,边长为4的正三角形DEF与正方形ABCD共有一顶点D,点E、F分别在线段AB、BC上,将点B与线段DF的中点G连接,则线段BG的长是$\sqrt{6}$+$\sqrt{2}$.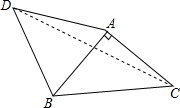 已知:如图,等腰直角△ABC,∠BAC=90°,AB=AC,点D为△ABC外一点,∠ADB=45°,连接CD,AD=4$\sqrt{2}$,CD=10,则AC=2$\sqrt{5}$.
已知:如图,等腰直角△ABC,∠BAC=90°,AB=AC,点D为△ABC外一点,∠ADB=45°,连接CD,AD=4$\sqrt{2}$,CD=10,则AC=2$\sqrt{5}$.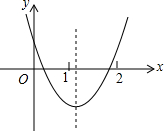 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:(1)4a+2b+c>0;(2)$\frac{ab}{c}$<0;(3)一次函数y=x+bc一定不过第二象限;(4)$\frac{4ac-{b}^{2}}{4a}$<a+b+c,其中正确的是①②③④.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:(1)4a+2b+c>0;(2)$\frac{ab}{c}$<0;(3)一次函数y=x+bc一定不过第二象限;(4)$\frac{4ac-{b}^{2}}{4a}$<a+b+c,其中正确的是①②③④.