题目内容
2.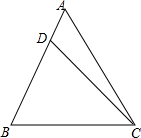 如图,在等边△ABC中,DB=2,∠DCB=45°,则CD=3$\sqrt{2}$-$\sqrt{6}$.
如图,在等边△ABC中,DB=2,∠DCB=45°,则CD=3$\sqrt{2}$-$\sqrt{6}$.
分析 过点D作DE⊥BC于点E,由∠DCB=45°可知△CDE为等腰直角三角形,设DE=a,则CE=a,CD=$\sqrt{2}$a,通过解直角三角形找出线段BE的长度,结合BC=BE+EC=2,即可得出关于a的一元一次方程,解方程即可得出a的值,由此即可得出结论.
解答 解:过点D作DE⊥BC于点E,如图所示.
∵DE⊥BC,∠DCE=45°,
∴△CDE为等腰直角三角形,
设DE=a,则CE=a,CD=$\sqrt{2}$a.
∵△ABC为等边三角形,
∴∠B=60°.
在Rt△BDE中,∠B=60°,∠BED=90°,DE=a,
∴BE=DE•cot∠B=$\frac{\sqrt{3}}{3}$a.
∵BC=BE+EC=$\frac{\sqrt{3}}{3}$a+a=2,即$\frac{3+\sqrt{3}}{3}$a=2,
解得:a=3-$\sqrt{3}$,
∴CD=$\sqrt{2}$a=3$\sqrt{2}$-$\sqrt{6}$.
故答案为:3$\sqrt{2}$-$\sqrt{6}$.
点评 本题考查了等边三角形的性质、解直角三角形以及解一元一次方程,解题的关键是求出线段DE的长度.本题属于基础题,难度不大,解决该题型题目时,根据等边三角形的性质找出角的度数,再通过解直角三角形求出边的长度是关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
13.化简$\sqrt{{x}^{4}+{x}^{2}{y}^{2}}$的结果是( )
| A. | x2+xy | B. | |x|$\sqrt{{x}^{2}+{y}^{2}}$ | C. | xy$\sqrt{{x}^{2}+1}$ | D. | x2y$\sqrt{x+1}$ |
12.下列命题是真命题的是( )
| A. | 非正数没有平方根 | B. | 相等的角不一定是对顶角 | ||
| C. | 同位角相等 | D. | 和为180°的两个角一定是邻补角 |
 如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=12cm,BC=13cm,AB=9cm,动点M从点A出发沿AD方向向点D以1cm/s的速度运动,动点N从点C开始沿着CB方向向点B以3cm/s的速度运动.点M,N分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.经过多长时间,四边形MNCD是平行四边形?求出此时四边形MNCD的面积.
如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=12cm,BC=13cm,AB=9cm,动点M从点A出发沿AD方向向点D以1cm/s的速度运动,动点N从点C开始沿着CB方向向点B以3cm/s的速度运动.点M,N分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.经过多长时间,四边形MNCD是平行四边形?求出此时四边形MNCD的面积.