题目内容
17. 如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=12cm,BC=13cm,AB=9cm,动点M从点A出发沿AD方向向点D以1cm/s的速度运动,动点N从点C开始沿着CB方向向点B以3cm/s的速度运动.点M,N分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.经过多长时间,四边形MNCD是平行四边形?求出此时四边形MNCD的面积.
如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=12cm,BC=13cm,AB=9cm,动点M从点A出发沿AD方向向点D以1cm/s的速度运动,动点N从点C开始沿着CB方向向点B以3cm/s的速度运动.点M,N分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.经过多长时间,四边形MNCD是平行四边形?求出此时四边形MNCD的面积.
分析 用t表示出MD、CN,然后根据平行四边形判定定理可得MD=CN,然后计算即可求出t的值,四边形MNCD的面积=CN•AB,即可得出结果.
解答 解:∵点M的速度为1cm/s,点N的速度为3cm/s,
∴MD=AD-AM=12-t,CN=3t,
∵AD∥BC,当MD=CN时,四边形MNCD是平行四边形
∴12-t=3t,
解得:t=3;
∴当t=3s时,四边形MNCD是平行四边形;
此时CN=9cm,
∴四边形MNCD的面积=CN•AB=9×9=81(cm2).
点评 本题考查了平行四边形的判定、平行四边形面积的计算;熟练掌握平行四边形的判定定理,由题意得出方程是解决问题的关键.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 如图,在?ABCD中,M,N分别是AD,BC的中点,连结AN,BM交于点P,连结CM,DN相交于点Q,则图中与△APM面积相等的三角形有几个?请一一列出,并说明理由.
如图,在?ABCD中,M,N分别是AD,BC的中点,连结AN,BM交于点P,连结CM,DN相交于点Q,则图中与△APM面积相等的三角形有几个?请一一列出,并说明理由.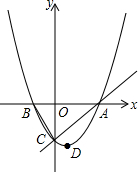 如图,已知抛物线y=ax2+bx+c的顶点D的坐标为(1,-$\frac{9}{2}$),且与x轴交于A,B两点,与y轴交于C点,A点的坐标为(4,0),P点是抛物线上的一个动点,且横坐标为m.
如图,已知抛物线y=ax2+bx+c的顶点D的坐标为(1,-$\frac{9}{2}$),且与x轴交于A,B两点,与y轴交于C点,A点的坐标为(4,0),P点是抛物线上的一个动点,且横坐标为m.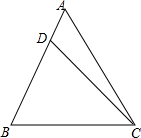 如图,在等边△ABC中,DB=2,∠DCB=45°,则CD=3$\sqrt{2}$-$\sqrt{6}$.
如图,在等边△ABC中,DB=2,∠DCB=45°,则CD=3$\sqrt{2}$-$\sqrt{6}$.