题目内容
14.已知x,y满足y=$\frac{\sqrt{{x}^{2}-9}+\sqrt{9-{x}^{2}}-1}{6+2x}$,求xy的值.分析 根据二次根式有意义的条件和分式有意义的条件可得$\left\{\begin{array}{l}{{x}^{2}-9≥0}\\{9-{x}^{2}≥0}\\{6+2x≠0}\end{array}\right.$,解不等式组可得x的值,进而可得y的值,代入即可求出答案.
解答 解:由题意得:$\left\{\begin{array}{l}{{x}^{2}-9≥0}\\{9-{x}^{2}≥0}\\{6+2x≠0}\end{array}\right.$,
解得:x=3,
则y=-$\frac{1}{12}$,
故xy=3×(-$\frac{1}{12}$)=-$\frac{1}{4}$.
点评 此题主要考查了二次根式有意义的条件和分式有意义的条件,关键是掌握二次根式中的被开方数是非负数,分式的分母不能为0.

练习册系列答案
相关题目
 如图,在?ABCD中,M,N分别是AD,BC的中点,连结AN,BM交于点P,连结CM,DN相交于点Q,则图中与△APM面积相等的三角形有几个?请一一列出,并说明理由.
如图,在?ABCD中,M,N分别是AD,BC的中点,连结AN,BM交于点P,连结CM,DN相交于点Q,则图中与△APM面积相等的三角形有几个?请一一列出,并说明理由.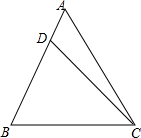 如图,在等边△ABC中,DB=2,∠DCB=45°,则CD=3$\sqrt{2}$-$\sqrt{6}$.
如图,在等边△ABC中,DB=2,∠DCB=45°,则CD=3$\sqrt{2}$-$\sqrt{6}$.