题目内容
5. 如图,每个小正方形的边长都是1的方格纸中,有线段AB和线段CD,点A、B、C、D的端点都在小正方形的顶点上.
如图,每个小正方形的边长都是1的方格纸中,有线段AB和线段CD,点A、B、C、D的端点都在小正方形的顶点上.(1)在方格纸中画出一个以线段AB为一边的菱形ABEF,所画的菱形的各顶点必须在小正方形的顶点上,并且其面积为20.
(2)在方格纸中以CD为底边画出等腰三角形CDK,点K在小正方形的顶点上,且△CDK的面积为10.
(3)在(1)、(2)的条件下,连接EK,请直接写出线段EK的长.
分析 (1)根据条件一个边长为5高为4的菱形即可.
(2)画一个等腰三角形,底为2$\sqrt{5}$,高为2$\sqrt{5}$即可.
(3)观察图象即可解决问题.
解答 解:(1)菱形ABEF如图所示.AB=BE=EF=AF=5,高为4,面积为20,满足条件.
(2)△CDK如图所示.S△CDK=$\frac{1}{2}$$•2\sqrt{5}$•2$\sqrt{5}$=10
(3)由图象可知,EK=2.
点评 本题考查作图设计由应用、菱形的性质、等腰三角形的性质等知识,解题的关键是先根据数量关系确定相关线段的长度,然后画出图形,体现了数形结合的思想,是一个好题目,中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.在平面直角坐标系中,把直线y=-2x+3沿y轴向上平移两个单位长度后,得到的直线的函数关系式为( )
| A. | y=-2x+1 | B. | y=-2x-5 | C. | y=-2x+5 | D. | y=-2x+7 |
20.已知Rt△ABC中,∠C=90°,AC=1,BC=3,则AB的取值范围是( )
| A. | 3.0<AB<3.1 | B. | 3.1<AB<3.2 | C. | 3.2<AB<3.3 | D. | 3.3<AB<3.4 |
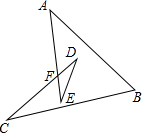 如图,求∠A+∠B+∠C+∠D+∠E的度数:180°.
如图,求∠A+∠B+∠C+∠D+∠E的度数:180°.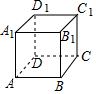 如图,已知正方体的棱长为2,则正方体表面上从A点到C点的最短距离为2$\sqrt{2}$.
如图,已知正方体的棱长为2,则正方体表面上从A点到C点的最短距离为2$\sqrt{2}$.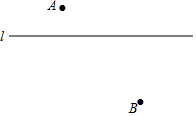 尺规作图(保留作图痕迹):如图,已知直线l及其两侧两点A、B.
尺规作图(保留作图痕迹):如图,已知直线l及其两侧两点A、B.