题目内容
5.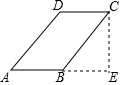 作平行四边形ABCD的高CE,B是AE的中点,如图.
作平行四边形ABCD的高CE,B是AE的中点,如图.(1)小琴说:如果连接DB,则DB⊥AE,对吗?说明理由.
(2)如果BE:CE=1:$\sqrt{2}$,BC=3cm,求AB.
分析 (1)直接利用平行四边形的性质得出BD∥CE,进而得出答案;
(2)直接利用勾股定理得出BE的长,进而得出答案.
解答  解:(1)对,
解:(1)对,
理由:∵ABCD是平行四边形,
∴CD∥AB且CD=AB.
又B是AE的中点,
∴CD∥BE且CD=BE.
∴BD∥CE,
∵CE⊥AE,
∴BD⊥AE;
(2)设BE=x,则CE=$\sqrt{2}$x,
在Rt△BEC中:x2+($\sqrt{2}$x)2=9,
解得:x=$\sqrt{3}$,
故AB=BE=$\sqrt{3}$(cm).
点评 此题主要考查了平行四边形的性质以及勾股定理,正确应用平行四边形的性质是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.下列说法不正确的是( )
| A. | 平行四边形的对边平行且相等 | B. | 平行四边形对角线互相平分 | ||
| C. | 平行四边形是轴对称图形 | D. | 平行四边形是中心对称图形 |
20.下列各命题不成立的是( )
| A. | 平行四边形的对边平行且相等 | |
| B. | 依次连结正方形各边中点所得的四边形是正方形 | |
| C. | 对角线互相平分且相等的四边形是矩形 | |
| D. | 对角线互相垂直平分的四边形是正方形 |
17.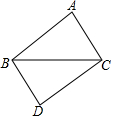 如图△ABC与△CDB中,AB=CD,要使△ABC≌△CDB,需要添加的条件是( )
如图△ABC与△CDB中,AB=CD,要使△ABC≌△CDB,需要添加的条件是( )
 如图△ABC与△CDB中,AB=CD,要使△ABC≌△CDB,需要添加的条件是( )
如图△ABC与△CDB中,AB=CD,要使△ABC≌△CDB,需要添加的条件是( )| A. | ∠A=∠D | B. | AC=BC | C. | ∠ACB=∠DBC | D. | ∠ABC=∠DCB |
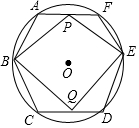 如图,⊙O半径为4cm,其内接正六边形ABCDEF,点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向终点F,C运动,连接PB,QE,PE,BQ.设运动时间为t(s).
如图,⊙O半径为4cm,其内接正六边形ABCDEF,点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向终点F,C运动,连接PB,QE,PE,BQ.设运动时间为t(s).