题目内容
17.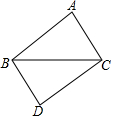 如图△ABC与△CDB中,AB=CD,要使△ABC≌△CDB,需要添加的条件是( )
如图△ABC与△CDB中,AB=CD,要使△ABC≌△CDB,需要添加的条件是( )| A. | ∠A=∠D | B. | AC=BC | C. | ∠ACB=∠DBC | D. | ∠ABC=∠DCB |
分析 可以添加条件:∠ABC=∠DCB,再根据题目条件AB=CD,再加上公共边BC=CB,可利用SAS证明△ABC≌△CDB.
解答 解:题中已有条件AB=CD,隐含公共边相等,那么就缺少这两边所夹的角相等,即∠ABC=∠DCB,
故选:D.
点评 此题主要考查了全等三角形的判定,关键是掌握判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
12.下列四个等式从左到右的变形,是多项式的因式分解的是( )
| A. | (x+3)(x-3)=x2-9 | B. | a2b+ab2=ab(a+b) | ||
| C. | x2-3x+1=x(x-3)+1 | D. | ${m^2}-2m-1=m(m-2-\frac{1}{m})$ |
2.下列运算正确的是( )
| A. | a2+a3=a5 | B. | 2a2-3a2=-a2 | C. | (a-2)2=a2-4 | D. | (a+1)(a-1)=a2-2 |
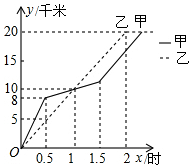 在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图中提供的信息,有下列说法:
在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图中提供的信息,有下列说法: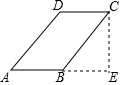 作平行四边形ABCD的高CE,B是AE的中点,如图.
作平行四边形ABCD的高CE,B是AE的中点,如图.
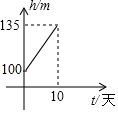
 如图,在平行四边形ABCE中,点D是AE上的一点,且CE=CD,求证:∠DCB=∠B.
如图,在平行四边形ABCE中,点D是AE上的一点,且CE=CD,求证:∠DCB=∠B.