题目内容
10．
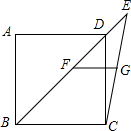如图，已知在正方形ABCD中，连接BD并延长至点E，连接CE，F、G分别为BE，CE的中点，连接FG，若AB=6，则FG的长度为3．
分析 根据正方形的性质得到FG∥BC，而FF、G分别为BE，CE的中点，则可得到FG为△BCE的中位线．
解答 解：∵正方形ABCD，
∴AB=BC=6，
∵F、G分别为BE，CE的中点，
∴FG=3，
故答案为：3
点评 本题考查了正方形的性质，三角形的中位线定理：三角形的中位线平行于底边，并且等于底边的一半．
练习册系列答案
相关题目
1．
如图，将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE，点B的对应点D恰好落在BC边上，若AB=1，∠B=60°，则△ACD的面积为（ ）
如图，将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE，点B的对应点D恰好落在BC边上，若AB=1，∠B=60°，则△ACD的面积为（ ）| A． | 2$\sqrt{3}$ | B． | $\sqrt{3}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{3}}{4}$ |
18．下列判断中，正确的是（ ）
| A． | 有理数是有限小数 | B． | 无理数都是无限小数 | ||
| C． | 无限小数是无理数 | D． | 无理数没有算术平方根 |
5．用配方解方程3x2-6x-1=0，则方程可变形为（ ）
| A． | （x-3）2=$\frac{1}{3}$ | B． | 3（x-1）2=$\frac{1}{3}$ | C． | （3x-1）2=1 | D． | （x-1）2=$\frac{4}{3}$ |
15．
如图，AB∥CD∥EF，则下列各式中正确的是（ ）
如图，AB∥CD∥EF，则下列各式中正确的是（ ）| A． | ∠1+∠3=180° | B． | ∠1+∠2=∠3 | C． | ∠2+∠3+∠1=180° | D． | ∠2+∠3-∠1=180° |
2．下列事件中，是必然事件的是（ ）
| A． | 掷一枚均匀的六面体骰子，骰子停止后朝上的点数是6 | |
| B． | 打开电视机，任意选择一个频道，正在播新闻 | |
| C． | 在地球上，抛出去的篮球会下落 | |
| D． | 随机地从0，1，2，…，9这十个数中选取两个数，和为20 |
如图所示，点C是线段AB上一点，AC＜CB，M、N分别是AB、CB的中点，AC=8，NB=5，则线段MN=4．
20．下列变形，正确的是（ ）
| A． | $\frac{by}{2ay}=\frac{b}{2a}$ | B． | $-\frac{y}{x}=\frac{-y}{-x}$ | ||
| C． | 1+$\frac{1}{a}$=$\frac{2}{a}$ | D． | $\frac{{{a^2}+ab}}{{{b^2}+ab}}=\frac{a^2}{b^2}$ |