��Ŀ����
10����1���ⷽ����$\left\{\begin{array}{l}{\frac{x}{2}-\frac{y+1}{3}=1}\\{3x+2y=2}\end{array}\right.$��2���ⲻ��ʽ��$\left\{\begin{array}{l}{5x+7��3��x+1��}\\{\frac{1}{2}x-1��1-\frac{3}{2}x}\end{array}\right.$
���ѽ⼯�������ϱ�ʾ������
���� ��1������ԭ������Ϊһ��ʽ�������üӼ���Ԫ�����ɵã�
��2���ֱ����ÿһ������ʽ�Ľ⼯�����ݿھ���ͬ��ȡ��ͬСȡС����СС���м��ҡ����СС����ȷ������ʽ��Ľ⼯��
��� �⣺��1��ԭ�����������ɵã�$\left\{\begin{array}{l}{3x-2y=8}&{��}\\{3x+2y=2}&{��}\end{array}\right.$��
��+�ڣ��ã�6x=10��
��ã�x=$\frac{5}{3}$��
��-�٣��ã�4y=-6��
��ã�y=-$\frac{3}{2}$��
����Ľ�Ϊ$\left\{\begin{array}{l}{x=\frac{5}{3}}\\{y=-\frac{3}{2}}\end{array}\right.$��
��2��$\left\{\begin{array}{l}{5x+7��3��x+1��}&{��}\\{\frac{1}{2}x-1��1-\frac{3}{2}x}&{��}\end{array}\right.$��
�ⲻ��ʽ�٣��ã�x��-2��
�ⲻ��ʽ�ڣ��ã�x��1��
���ʽ��Ľ⼯Ϊ-2��x��1��
���⼯��ʾ�����������£�
���� ���⿼����ǽ��Ԫһ�η������һԪһ�β���ʽ�飬��ȷ���ÿһ������ʽ�⼯�ǻ�������֪��ͬ��ȡ��ͬСȡС����СС���м��ң����СС�Ҳ�������ԭ���ǽ�����Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
1�� ��ͼ����������ABCD��һ��ABΪ���������ȱߡ�ABE�����BED�Ķ����ǣ�������
��ͼ����������ABCD��һ��ABΪ���������ȱߡ�ABE�����BED�Ķ����ǣ�������
 ��ͼ����������ABCD��һ��ABΪ���������ȱߡ�ABE�����BED�Ķ����ǣ�������
��ͼ����������ABCD��һ��ABΪ���������ȱߡ�ABE�����BED�Ķ����ǣ�������| A�� | 30�� | B�� | 37.5�� | C�� | 45�� | D�� | 50�� |
18��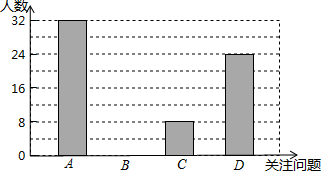 6��5�������绷���գ�2017�����绷�����й��������ǡ���ˮ��ɽ���ǽ�ɽ��ɽ����С������ѧϰ�������������ĸ����棨A-������Ⱦ��B-��ˮ��ԴΣ����C-���ػ�Į����D-ȫ���ů����ȫУͬѧ����������������飬�˽����������ĸ����������ע�����⣨ÿ����ѡһ��������������²�������ͳ��ͼ����
6��5�������绷���գ�2017�����绷�����й��������ǡ���ˮ��ɽ���ǽ�ɽ��ɽ����С������ѧϰ�������������ĸ����棨A-������Ⱦ��B-��ˮ��ԴΣ����C-���ػ�Į����D-ȫ���ů����ȫУͬѧ����������������飬�˽����������ĸ����������ע�����⣨ÿ����ѡһ��������������²�������ͳ��ͼ����
����ͼ������������⣺
��1�����е�b=80��n=0.3��
��2��������ͳ��ͼ����������
��3����С�����ڵ�ѧУ��1100��ѧ������ô����С���ṩ����Ϣ���Ƹ�У��ע��������Ⱦ����ѧ����Լ�ж����ˣ�
 6��5�������绷���գ�2017�����绷�����й��������ǡ���ˮ��ɽ���ǽ�ɽ��ɽ����С������ѧϰ�������������ĸ����棨A-������Ⱦ��B-��ˮ��ԴΣ����C-���ػ�Į����D-ȫ���ů����ȫУͬѧ����������������飬�˽����������ĸ����������ע�����⣨ÿ����ѡһ��������������²�������ͳ��ͼ����
6��5�������绷���գ�2017�����绷�����й��������ǡ���ˮ��ɽ���ǽ�ɽ��ɽ����С������ѧϰ�������������ĸ����棨A-������Ⱦ��B-��ˮ��ԴΣ����C-���ػ�Į����D-ȫ���ů����ȫУͬѧ����������������飬�˽����������ĸ����������ע�����⣨ÿ����ѡһ��������������²�������ͳ��ͼ����| ��ע������ | Ƶ�� | Ƶ�� |
| A | 32 | m |
| B | a | 0.2 |
| C | 8 | 0.1 |
| D | 24 | n |
| �ϼ� | b | 1 |
��1�����е�b=80��n=0.3��
��2��������ͳ��ͼ����������
��3����С�����ڵ�ѧУ��1100��ѧ������ô����С���ṩ����Ϣ���Ƹ�У��ע��������Ⱦ����ѧ����Լ�ж����ˣ�
19��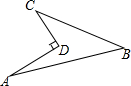 ��ͼ��ʾ��һ��أ���֪��ADC=90�㣬AD=12m��CD=9m��AB=25m��BC=20m�������ص����Ϊ��������ƽ���ף�
��ͼ��ʾ��һ��أ���֪��ADC=90�㣬AD=12m��CD=9m��AB=25m��BC=20m�������ص����Ϊ��������ƽ���ף�
 ��ͼ��ʾ��һ��أ���֪��ADC=90�㣬AD=12m��CD=9m��AB=25m��BC=20m�������ص����Ϊ��������ƽ���ף�
��ͼ��ʾ��һ��أ���֪��ADC=90�㣬AD=12m��CD=9m��AB=25m��BC=20m�������ص����Ϊ��������ƽ���ף�| A�� | 96 | B�� | 204 | C�� | 196 | D�� | 304 |
