题目内容
9.已知x、y是实数,且$\root{3}{z}$=2,y=$\sqrt{x-2}$+$\sqrt{2-x}$+$\frac{1}{4}$,则$\sqrt{{y^2}-4y+4}$-(x-2+$\sqrt{2}}$)2-z=-8$\frac{1}{4}$.分析 根据二次根式有意义的条件可得x=2,进而可得y=$\frac{1}{4}$,再根据立方根可得z=8,然后再代入可得$\sqrt{{y^2}-4y+4}$-(x-2+$\sqrt{2}}$)2-z的值.
解答 解:由题意得:$\left\{\begin{array}{l}{x-2≥0}\\{2-x≥0}\end{array}\right.$,
解得:x=2,
∴y=$\frac{1}{4}$,
∵$\root{3}{z}$=2,
∴z=8,
$\sqrt{{y^2}-4y+4}$-(x-2+$\sqrt{2}}$)2-z═|y-2|-2-8=1$\frac{3}{4}$-10=-8$\frac{1}{4}$,
故答案为:-8$\frac{1}{4}$.
点评 此题主要考查了二次根式有意义的条件,以及实数的运算,关键是掌握二次根式中的被开方数是非负数.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.某校在“爱护地球、绿化祖国”的创建活动中,组织学生开展了植树造林活动,为了了解全校学生的植树情况,学校随机抽查了100名学生的植树情况,将调查数据整理如表:
(1)上述数据中,中位数是5,众数是4.
(2)若该校有1680名学生,请根据以上调查结果估计该校学生的植树总数.
| 植树数量(棵) | 4 | 5 | 6 | 8 | 10 |
| 人数 | 30 | 26 | 25 | 15 | 8 |
(2)若该校有1680名学生,请根据以上调查结果估计该校学生的植树总数.
14.某公司招聘一名公关人员,应聘者小王参加面试和笔试,成绩(100分制)如表所示:
(1)请计算小王面试平均成绩;
(2)如果面试平均成绩与笔试成绩按6:4的比确定,请计算出小王的最终成绩.
| 面试 | 笔试 | |||
| 成绩 | 评委1 | 评委2 | 评委3 | 92 |
| 88 | 90 | 86 | ||
(2)如果面试平均成绩与笔试成绩按6:4的比确定,请计算出小王的最终成绩.
1. 如图,以正方形ABCD的一边AB为边向外作等边△ABE,则∠BED的度数是( )
如图,以正方形ABCD的一边AB为边向外作等边△ABE,则∠BED的度数是( )
 如图,以正方形ABCD的一边AB为边向外作等边△ABE,则∠BED的度数是( )
如图,以正方形ABCD的一边AB为边向外作等边△ABE,则∠BED的度数是( )| A. | 30° | B. | 37.5° | C. | 45° | D. | 50° |
18.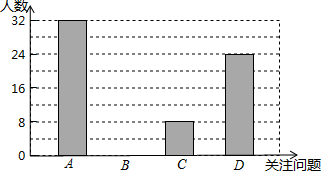 6月5日是世界环境日,2017年世界环境日中国的主题是“绿水青山就是金山银山”,小明积极学习与宣传,并从四个方面(A-空气污染,B-淡水资源危机,C-土地荒漠化,D-全球变暖)对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),并绘制了如下不完整的统计图表:
6月5日是世界环境日,2017年世界环境日中国的主题是“绿水青山就是金山银山”,小明积极学习与宣传,并从四个方面(A-空气污染,B-淡水资源危机,C-土地荒漠化,D-全球变暖)对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),并绘制了如下不完整的统计图表:
请结合图表完成下列问题:
(1)表中的b=80,n=0.3;
(2)将条形统计图补充完整;
(3)若小明所在的学校有1100名学生,那么根据小明提供的信息估计该校关注“空气污染”的学生大约有多少人?
 6月5日是世界环境日,2017年世界环境日中国的主题是“绿水青山就是金山银山”,小明积极学习与宣传,并从四个方面(A-空气污染,B-淡水资源危机,C-土地荒漠化,D-全球变暖)对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),并绘制了如下不完整的统计图表:
6月5日是世界环境日,2017年世界环境日中国的主题是“绿水青山就是金山银山”,小明积极学习与宣传,并从四个方面(A-空气污染,B-淡水资源危机,C-土地荒漠化,D-全球变暖)对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),并绘制了如下不完整的统计图表:| 关注的问题 | 频数 | 频率 |
| A | 32 | m |
| B | a | 0.2 |
| C | 8 | 0.1 |
| D | 24 | n |
| 合计 | b | 1 |
(1)表中的b=80,n=0.3;
(2)将条形统计图补充完整;
(3)若小明所在的学校有1100名学生,那么根据小明提供的信息估计该校关注“空气污染”的学生大约有多少人?
19.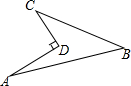 如图所示的一块地,已知∠ADC=90°,AD=12m,CD=9m,AB=25m,BC=20m,则这块地的面积为( )平方米.
如图所示的一块地,已知∠ADC=90°,AD=12m,CD=9m,AB=25m,BC=20m,则这块地的面积为( )平方米.
 如图所示的一块地,已知∠ADC=90°,AD=12m,CD=9m,AB=25m,BC=20m,则这块地的面积为( )平方米.
如图所示的一块地,已知∠ADC=90°,AD=12m,CD=9m,AB=25m,BC=20m,则这块地的面积为( )平方米.| A. | 96 | B. | 204 | C. | 196 | D. | 304 |
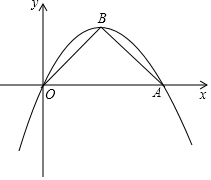 如图,在平面直角坐标系xOy,已知二次函数y=-$\frac{1}{2}$x2+bx的图象过点A(4,0),顶点为B,连接AB、BO.
如图,在平面直角坐标系xOy,已知二次函数y=-$\frac{1}{2}$x2+bx的图象过点A(4,0),顶点为B,连接AB、BO.