题目内容
20. 在平行四边形ABCD中,AB=2AD.
在平行四边形ABCD中,AB=2AD.(1)作AE平分∠BAD交DC于E(尺规作图,保留作图痕迹);
(2)在(1)的条件下,连接BE,判定△ABE的形状.(不要求证明).
分析 (1)根据角平分线的作法作∠BAD的平分线即可;
(2)延长AE交BC的延长线于点F,先由角平分线的性质得出∠DAE=∠BAE,再由平行线的性质得出∠BAE=∠DEA,故可得出∠DAE=∠DEA,故AD=DE,根据CD=2AD可知DE=CE,利用ASA定理得出△ADE≌△FCE,AD=CF,AE=EF,即△ABF是等腰三角形,据此可知BE⊥AF,△ABE是直角三角形.
解答 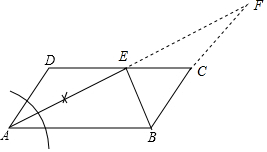 解:(1)如图,AE为所求;
解:(1)如图,AE为所求;
(2)△ABE为直角三角形.
理由:延长AE交BC的延长线于点F,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE.
∵四边形ABCD是平行四边形,
∴∠BAE=∠DEA,∠D=∠ECF,
∴∠DAE=∠DEA,
∴AD=DE.
∵CD=2AD,
∴DE=CE,
在△ADE与△FCE中,
∵$\left\{\begin{array}{l}{∠D=∠ECF}\\{DE=CE}\\{∠DEA=∠CEF}\end{array}\right.$,
∴△ADE≌△FCE(ASA),
∴AD=CF,AE=EF,
∴△ABF是等腰三角形,
∴BE⊥AF,即△ABE是直角三角形.
点评 本题考查的是作图-基本作图,熟知角平分线的作法是解答此题的关键.

练习册系列答案
相关题目
10.在平面直角坐标系中,点A、B的坐标分别为(-3,0)、(3,0),点P在反比例函数y=$\frac{9}{x}$的图象上.若△PAB为直角三角形,则满足条件的点P的个数为( )
| A. | 2个 | B. | 4个 | C. | 5个 | D. | 6个 |
4.2015年日照市人民政府投入1000万元用于改造乡村小学班班通工程建设,计划到2017年再追加投资210万元,如果每年的平均增长率相同,那么我市这两年该项投入的平均增长率为( )
| A. | 1.21% | B. | 8% | C. | 10% | D. | 12.1% |
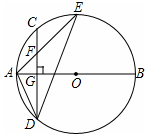 如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{DF}=\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=3,AF=4.
如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{DF}=\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=3,AF=4.
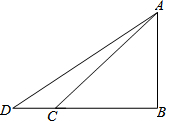 如图,要测量旗杆AB的高度,在地面C点处测得旗杆顶部A点的仰角为45°,从C点向外走2米到D点处,(B、C、D三点在同一直线上)测得旗杆顶部A点的仰角为37°,求旗杆AB的高度.
如图,要测量旗杆AB的高度,在地面C点处测得旗杆顶部A点的仰角为45°,从C点向外走2米到D点处,(B、C、D三点在同一直线上)测得旗杆顶部A点的仰角为37°,求旗杆AB的高度.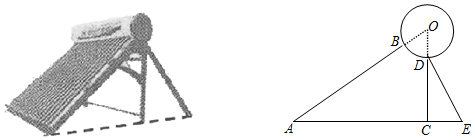
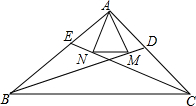 在△ABC中,BD平分∠ABC,CE平分∠ACB,过点A分别作BD,CE的垂线,垂足分别为点M,N,连接MN.求证:MN=$\frac{1}{2}(AB+AC-BC)$.
在△ABC中,BD平分∠ABC,CE平分∠ACB,过点A分别作BD,CE的垂线,垂足分别为点M,N,连接MN.求证:MN=$\frac{1}{2}(AB+AC-BC)$.