题目内容
3.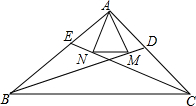 在△ABC中,BD平分∠ABC,CE平分∠ACB,过点A分别作BD,CE的垂线,垂足分别为点M,N,连接MN.求证:MN=$\frac{1}{2}(AB+AC-BC)$.
在△ABC中,BD平分∠ABC,CE平分∠ACB,过点A分别作BD,CE的垂线,垂足分别为点M,N,连接MN.求证:MN=$\frac{1}{2}(AB+AC-BC)$.
分析 延长AM、AN交BC于F、G.根据ASA发现两对全等三角形,根据全等三角形的性质得到MN是三角形AFG的中位线,同时得到FG的长,根据三角形的中位线定理即可计算.
解答 解:延长AM、AN交BC于F、G.
∵BD平分∠ABC,CE平分∠ACB,过点A分别作BD,CE的垂线,垂足分别为点M,N,
∴∠ABM=∠FBM,BM=BM,∠AMB=∠FMB,
在△AMB和△FMB中
$\left\{\begin{array}{l}{∠ABM=∠FBM}\\{BM=BM}\\{∠AMB=∠FMB}\end{array}\right.$
∴△AMB≌△FBM,
∴AM=FM,BF=AB.
同理AN=NG,CG=AC.
∴MN=$\frac{1}{2}$FG=$\frac{1}{2}$(AB+AC-BC).
点评 此题综合考查了全等三角形的判定和性质、三角形的中位线定理,解此题的关键是求出AN=NG和AM=MF.

练习册系列答案
相关题目
17. 如图有矩形纸片ABCD,AB=6,BC=8,对折纸片使AD与BC重合得到折痕EF,把纸片展平,再一次折叠纸片,使点B落在EF上,并使折痕经过点A,得到折痕AG,则HF=( )
如图有矩形纸片ABCD,AB=6,BC=8,对折纸片使AD与BC重合得到折痕EF,把纸片展平,再一次折叠纸片,使点B落在EF上,并使折痕经过点A,得到折痕AG,则HF=( )
 如图有矩形纸片ABCD,AB=6,BC=8,对折纸片使AD与BC重合得到折痕EF,把纸片展平,再一次折叠纸片,使点B落在EF上,并使折痕经过点A,得到折痕AG,则HF=( )
如图有矩形纸片ABCD,AB=6,BC=8,对折纸片使AD与BC重合得到折痕EF,把纸片展平,再一次折叠纸片,使点B落在EF上,并使折痕经过点A,得到折痕AG,则HF=( )| A. | 3 | B. | 4.5 | C. | 8-3$\sqrt{3}$ | D. | 8-2$\sqrt{3}$ |
12.下列关于x的一元二次方程中,有两个相等实数根的是( )
| A. | x2+1=0 | B. | x2+x-1=0 | C. | x2+2x-3=0 | D. | 4x2-4x+1=0 |
 在平行四边形ABCD中,AB=2AD.
在平行四边形ABCD中,AB=2AD.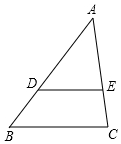 如图,在△ABC中,DE∥BC,AD=2BD,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,那么$\overrightarrow{DE}$=$-\frac{2}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$.
如图,在△ABC中,DE∥BC,AD=2BD,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,那么$\overrightarrow{DE}$=$-\frac{2}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$.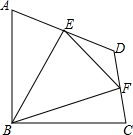 如图,在四边形ABCD中,∠ABC=90°,AB=BC=2$\sqrt{2}$,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,求△BEF的面积.
如图,在四边形ABCD中,∠ABC=90°,AB=BC=2$\sqrt{2}$,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,求△BEF的面积.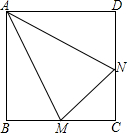 如图,M、N分别是正方形ABCD的边BC、CD上的点,已知:∠MAN=30°,AM=AN,△AMN的面积为1.
如图,M、N分别是正方形ABCD的边BC、CD上的点,已知:∠MAN=30°,AM=AN,△AMN的面积为1.