题目内容
11.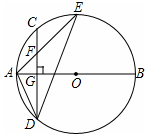 如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{DF}=\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=3,AF=4.
如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{DF}=\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=3,AF=4.(1)求证:△ADF∽△AED;
(2)求FG的长;
(3)求tan∠E的值.
分析 (1)根据垂径定理可知,∠ADF=∠AED,又因为∵∠FAD=∠DAE,从而可知△ADF∽△AED;
(2)由题意可求出DF的长度为9,从而可求出CD的长度为12,由垂径定理可知:CG=DG=6,所以FG=CG-CF=3;
(3)由勾股定理可求出AG的长度,由圆周角定理可知∠E=∠ADF,从而可求出tan∠E的值.
解答 解:(1)∵AB是⊙O的直径,弦CD⊥AB,
∴DG=CG,
∴∠ADF=∠AED,
∵∠FAD=∠DAE
∴△ADF∽△AED;
(2)∵$\frac{CF}{DF}=\frac{1}{3}$,CF=3,
∴DF=9,
∴CD=CF+DF=12,
∴CG=DG=6,
∴FG=CG-CF=3,
(3)∵AF=4,FG=3,
∴AG=$\sqrt{A{F^2}-F{G^2}}=\sqrt{7}$,
由(1)可知:∠E=∠ADF,
∴tanE=$tan∠ADF=\frac{AG}{DG}=\frac{{\sqrt{7}}}{6}$
点评 本题考查圆的综合问题,涉及勾股定理,垂径定理,相似三角形的判定,锐角三角函数,本题综合考查学生灵活运用知识的能力.

练习册系列答案
相关题目
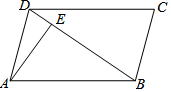 如图,在?ABCD中,DB=DC,∠C的度数比∠ABD的度数大54°,AE⊥BD于点E,则∠DAE的度数等于12°.
如图,在?ABCD中,DB=DC,∠C的度数比∠ABD的度数大54°,AE⊥BD于点E,则∠DAE的度数等于12°. 在平行四边形ABCD中,AB=2AD.
在平行四边形ABCD中,AB=2AD.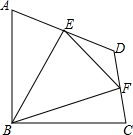 如图,在四边形ABCD中,∠ABC=90°,AB=BC=2$\sqrt{2}$,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,求△BEF的面积.
如图,在四边形ABCD中,∠ABC=90°,AB=BC=2$\sqrt{2}$,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,求△BEF的面积.