Question

8．如图，在平面直角坐标系内，已知直线l₁经过原点O 及A（2，2$\sqrt{3}$）两点，将直线l₁向右平移4个单位后得到直线l₂，直线l₂与x 轴交于点B．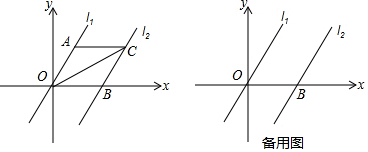

（1）求直线l₂的函数表达式；
（2）作∠AOB 的平分线交直线l₂于点C，连接AC．求证：四边形OACB是菱形；
（3）设点P 是直线l₂上一点，以P 为圆心，PB 为半径作⊙P，当⊙P 与直线l₁相切时，请求出圆心P 点的坐标．

Answer 1

分析 （1）过点A作AD⊥x轴于点D，设直线l₂与y轴交于点E，由A的坐标可知AD与OD的长度，进而求出E的坐标，利用待定系数法即可求出直线l₂的解析式．
（2）由角平分线的性质可知：∠AOC=∠BOC，过点C作CG⊥x轴于点G，由于l₂∥l₁，所以∠AOC=∠BCO，从而可知：∠BOC=∠BCO，过点C作CG⊥x轴于点G，求出A、C的坐标可知两点的纵坐标相等，从而可知AC∥OB，由于OB=OC，所以四边形OACB是菱形；
（3）由于点P的位置不确定，故需要分两种情况讨论，一是点P在x轴上方，二是点P在x轴下方，然后根据切线的性质即可求出P的坐标．

解答 （1）解：过点A作AD⊥x轴于点D，设直线l₂与y轴交于点E，（如图1）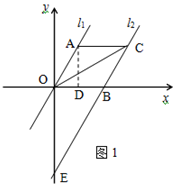
∵A（2，$2\sqrt{3}$），
∴AD=$2\sqrt{3}$，OD=2，
∵l₂∥l₁，
∴∠OBE=∠AOD，
∴tan∠OBE=tan∠AOD=$\frac{AD}{OD}=\sqrt{3}$，
∵OB=4，
∴OE=$\sqrt{3}$OB=$4\sqrt{3}$，
∴B（4，0）、E（0，$-4\sqrt{3}$），
设直线l₂为y=kx+b，则$\left\{\begin{array}{l}4k+b=0\\ b=-4\sqrt{3}\end{array}\right.$，
解得：$\left\{\begin{array}{l}k=\sqrt{3}\\ b=-4\sqrt{3}\end{array}\right.$，
∴直线l₂的函数表达式为$y=\sqrt{3}x-4\sqrt{3}$．

（2）证明：∵OC平分∠AOB，
∴∠AOC=∠BOC，
∵l₂∥l₁，
∴∠AOC=∠BCO，
∴∠BOC=∠BCO，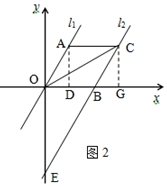
∴BC=OB=4，
过点C作CG⊥x轴于点G，（如图2）
∵∠CBG=∠AOD=60°，
∴CG=$\frac{{\sqrt{3}}}{2}BC=2\sqrt{3}$，BG=$\frac{1}{2}BC=2$，
∴OG=OB+BG=4+2=6，
∴C（6，$2\sqrt{3}$），
∵A（2，$2\sqrt{3}$），
∴AC∥OB，
∵BC∥OA，
∴四边形OACB是平行四边形，
∵OB=BC，
∴四边形OACB是菱形．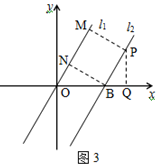

（3）解：当点P在x轴上方时，
过点P作PM⊥l₁于点M，过点B作BN⊥l₁于点N，过点PQ⊥x轴于点Q，（如图3）
则 PB=PM=BN=OBsin∠BOM=4sin60°=$2\sqrt{3}$，
∴PQ=PBsin∠PBQ=$2\sqrt{3}$sin60°=3，
BQ=PBcos∠PBQ=$2\sqrt{3}$cos60°=$\sqrt{3}$，
∴OQ=OB+BQ=4+$\sqrt{3}$，
∴P（4+$\sqrt{3}$，3），
当点P在x轴下方时，同理可得P（4-$\sqrt{3}$，-3），
∴点P的坐标为（4+$\sqrt{3}$，3）或P（4-$\sqrt{3}$，-3）

点评 本题考查圆的综合问题，涉及菱形的判定，锐角三角函数，待定系数法求解析式，切线的性质等知识，综合程度较高，考查学生灵活运用知识的能力．