题目内容
12.如图是某品牌太阳能热水器的实物图和横断面示意图,已知真空集热管AB与支架CD所在直线相交于水箱横断面⊙O的圆心,支架CD与水平面AE垂直,AB=110厘米,∠BAC=37°,垂直支架CD=57厘米,DE是另一根辅助支架,且∠CED=60°.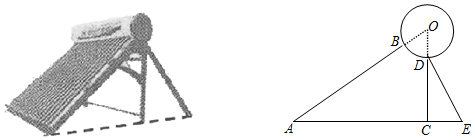
(1)求辅助支架DE长度;(结果保留根号)
(2)求水箱半径OD的长度.(结果精确到1厘米,参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
分析 (1)直接利用锐角三角函数关系得出DE=$\frac{DC}{sin∠E}$,进而得出答案;
(2)利用sin∠A=$\frac{CO}{AO}$,得出圆的半径,进而得出答案.
解答 解:(1)在Rt△DCE中,sin∠E=$\frac{CD}{DE}$,
∴DE=$\frac{DC}{sin∠E}$=$\frac{57}{sin60°}$=38$\sqrt{3}$(厘米),
答:辅助支架DE长度38$\sqrt{3}$厘米;
(2)设圆O的半径为x厘米,
在Rt△AOC中,sin∠A=$\frac{CO}{AO}$,
即sin37°=$\frac{57+x}{110+x}$,
∴$\frac{57+x}{110+x}$=$\frac{3}{5}$,
解得:x=22.5≈23(厘米),
答:水箱半径OD的长度为23厘米.
点评 此题主要考查了解直角三角形的应用,正确应用锐角三角函数关系是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17. 如图有矩形纸片ABCD,AB=6,BC=8,对折纸片使AD与BC重合得到折痕EF,把纸片展平,再一次折叠纸片,使点B落在EF上,并使折痕经过点A,得到折痕AG,则HF=( )
如图有矩形纸片ABCD,AB=6,BC=8,对折纸片使AD与BC重合得到折痕EF,把纸片展平,再一次折叠纸片,使点B落在EF上,并使折痕经过点A,得到折痕AG,则HF=( )
 如图有矩形纸片ABCD,AB=6,BC=8,对折纸片使AD与BC重合得到折痕EF,把纸片展平,再一次折叠纸片,使点B落在EF上,并使折痕经过点A,得到折痕AG,则HF=( )
如图有矩形纸片ABCD,AB=6,BC=8,对折纸片使AD与BC重合得到折痕EF,把纸片展平,再一次折叠纸片,使点B落在EF上,并使折痕经过点A,得到折痕AG,则HF=( )| A. | 3 | B. | 4.5 | C. | 8-3$\sqrt{3}$ | D. | 8-2$\sqrt{3}$ |
 在平行四边形ABCD中,AB=2AD.
在平行四边形ABCD中,AB=2AD.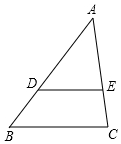 如图,在△ABC中,DE∥BC,AD=2BD,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,那么$\overrightarrow{DE}$=$-\frac{2}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$.
如图,在△ABC中,DE∥BC,AD=2BD,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,那么$\overrightarrow{DE}$=$-\frac{2}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$.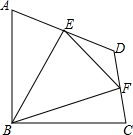 如图,在四边形ABCD中,∠ABC=90°,AB=BC=2$\sqrt{2}$,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,求△BEF的面积.
如图,在四边形ABCD中,∠ABC=90°,AB=BC=2$\sqrt{2}$,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,求△BEF的面积.