题目内容
2.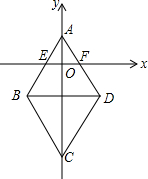 已知:如图,菱形ABCD中,已知点A(0,4)和C(0,-12),边AD交x轴于点F(3,0),求点B、D的坐标.
已知:如图,菱形ABCD中,已知点A(0,4)和C(0,-12),边AD交x轴于点F(3,0),求点B、D的坐标.
分析 直接利用菱形的性质得出N点坐标,再利用相似三角形的判定与性质得出ND的长,即可得出B,D点坐标.
解答 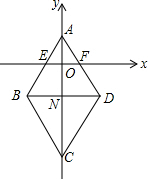 解:∵点A(0,4)和C(0,-12),
解:∵点A(0,4)和C(0,-12),
∴AC=16,
∴NC=8,故N(0,-4),
∵EF∥BD,
∴△AOF∽△AND,
∴$\frac{FO}{ND}$=$\frac{AO}{AN}$,
即$\frac{3}{ND}$=$\frac{4}{8}$,
解得:ND=6,
∴B(-6,-4),D(6,-4).
点评 此题主要考查了菱形的性质以及相似三角形的判定与性质,得出N点坐标是解题关键.

练习册系列答案
相关题目
13.一个圆锥的主视图是边长为4的等边三角形,这个这个圆锥的侧面积为( )
| A. | (4$\sqrt{3}$+4)π | B. | (8$\sqrt{3}$+4)π | C. | 12π | D. | 8π |
17.已知两点A(4,6),B(6,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则点A的对应点C的坐标为( )
| A. | (2,3) | B. | (3,1) | C. | (2,1) | D. | (3,3) |
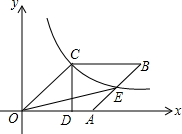 如图,已知四边形OABC是菱形,CD⊥x轴,垂足为D,函数$y=\frac{4}{x}$的图象经过点C,且与AB交于点E.若OD=2,则△OAE的面积为2$\sqrt{3}$-2.
如图,已知四边形OABC是菱形,CD⊥x轴,垂足为D,函数$y=\frac{4}{x}$的图象经过点C,且与AB交于点E.若OD=2,则△OAE的面积为2$\sqrt{3}$-2.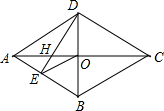 如图,四边形ABCD是菱形,对角线AC与BD相交于点O.DE⊥AB于点E.连接OE.
如图,四边形ABCD是菱形,对角线AC与BD相交于点O.DE⊥AB于点E.连接OE.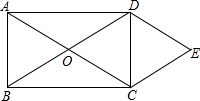 如图,已知O为矩形ABCD对角线的交点,过点D作DE∥AC,过点C作CE∥BD,且DE、CE相交于E点.
如图,已知O为矩形ABCD对角线的交点,过点D作DE∥AC,过点C作CE∥BD,且DE、CE相交于E点.
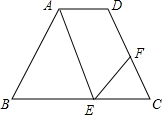 如图,AD∥BC,∠EAD=∠C,∠FEC=∠BAE,∠EFC=50°
如图,AD∥BC,∠EAD=∠C,∠FEC=∠BAE,∠EFC=50°