题目内容
 如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AB,BD,BC,AC的中点.求证:四边形EFGH是平行四边形.
如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AB,BD,BC,AC的中点.求证:四边形EFGH是平行四边形.考点:中点四边形
专题:
分析:根据中位线的判定GH=EF=
AB,EH=FG=
AB,从而得到EF∥GH,EF=GH,所以四边形EFGH是平行四边形.
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:∵E、F分别是AD,BD的中点,G、H分别中BC,AC的中点,
∴EF∥AB,EF=
AB;GH∥AB,GH=
AB,
∴EF∥GH,EF=GH.
∴四边形EFGH是平行四边形.
∴EF∥AB,EF=
| 1 |
| 2 |
| 1 |
| 2 |
∴EF∥GH,EF=GH.
∴四边形EFGH是平行四边形.
点评:此题考查了中点四边形的知识,了解平行四边形的判定后解此类问题就轻而易举了.

练习册系列答案
相关题目
 已知MN是线段AB的垂直平分线,C,D是MN上的两点.求证:
已知MN是线段AB的垂直平分线,C,D是MN上的两点.求证:
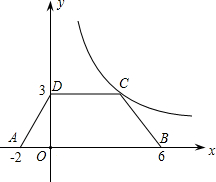 如图,等腰梯形ABCD放置在平面坐标系中,已知A(-2,0)、B(6,0)、D(0,3),反比例函数的图象经过点C.
如图,等腰梯形ABCD放置在平面坐标系中,已知A(-2,0)、B(6,0)、D(0,3),反比例函数的图象经过点C. 如图,OB是⊙O的半径,点C、D在⊙O上,∠DCB=27°,则∠DOB=
如图,OB是⊙O的半径,点C、D在⊙O上,∠DCB=27°,则∠DOB=