题目内容
如图1,在菱形OABC中,已知OA=2
,∠AOC=60°,抛物线y=ax2+bx+c(a≠0)经过O,C,B三点.
(Ⅰ)求出点B、C的坐标并求抛物线的解析式.
(Ⅱ)如图2,点E是AC的中点,点F是AB的中点,直线AG垂直BC于点G,点P在直线AG上.
(1)当OP+PC的最小值时,求出点P的坐标;
(2)在(1)的条件下,连接PE、PF、EF得△PEF,问在抛物线上是否存在点M,使得以M,B,C为顶点的三角形与△PEF相似?若存在,请求出点M的坐标;若不存在,请说明理由.

| 3 |
(Ⅰ)求出点B、C的坐标并求抛物线的解析式.
(Ⅱ)如图2,点E是AC的中点,点F是AB的中点,直线AG垂直BC于点G,点P在直线AG上.
(1)当OP+PC的最小值时,求出点P的坐标;
(2)在(1)的条件下,连接PE、PF、EF得△PEF,问在抛物线上是否存在点M,使得以M,B,C为顶点的三角形与△PEF相似?若存在,请求出点M的坐标;若不存在,请说明理由.

考点:二次函数综合题,等腰三角形的性质,菱形的性质,相似三角形的判定
专题:代数几何综合题,压轴题
分析:(Ⅰ)作CH⊥OA于点H,通过解三角函数求得A、C的坐标,由菱形的性质得出B点的坐标,然后应用待定系数法即可求得解析式.
(Ⅱ)(1)先求得抛物线的顶点坐标和与x轴的另一个交点坐标,当OP+PC最小时,由对称性可知,OP+PC=OB.由于OB是菱形ABCO的对角线,即可求得∠AOB=30°,然后通过解直角三角函数即可求得AP的长,进而求得P点的坐标;
(2)先求得△PEF是底角为30°的等腰三角形,根据OC=BC=BD=2
,∠BOC=∠BDC=30°,求得△OBC∽△BCD∽△PEF,又因为AQ=4,AG=3,BC=2
,所以GQ=1,BG=
,所以,tan∠GBQ=
=
,即∠GBQ=30°,得出△BQC也是底角为30°的等腰三角形,即可求得符合条件的点M的坐标.
(Ⅱ)(1)先求得抛物线的顶点坐标和与x轴的另一个交点坐标,当OP+PC最小时,由对称性可知,OP+PC=OB.由于OB是菱形ABCO的对角线,即可求得∠AOB=30°,然后通过解直角三角函数即可求得AP的长,进而求得P点的坐标;
(2)先求得△PEF是底角为30°的等腰三角形,根据OC=BC=BD=2
| 3 |
| 3 |
| 3 |
| 1 | ||
|
| ||
| 3 |
解答: 解:(Ⅰ)如图1,作CH⊥OA于点H,
解:(Ⅰ)如图1,作CH⊥OA于点H,
四边形OABC是菱形,OA=2
,∠AOC=60°,OC=2
,
OH=sin60°•2
=
,
CH=cos60°•2
=3,
A点坐标为(2
,0),
C点的坐标为(
,3),
由菱形的性质得B点的坐标为(3
,3).
设抛物线的解析式为y=ax2+bx+c,根据题意得
,
解得a=-
,b=
,c=0,
所以,y=-
x2+
x.
(Ⅱ)(1)如图2,由(Ⅰ)知抛物线的解析式为:y=-
x2+
x,
即对称轴为x=2
,顶点为Q(2
,4).
设抛物线与x轴的另一个交点为D,令y=0,得,x2-4
x=0,
解得x1=0,x2=4
,
即点D的坐标为(4
,0),
∵点A的坐标为(2
,0),对称轴为x=2
,
且AG⊥BC,
∴直线AG为抛物线的对称轴.
∵B、C两点关于直线AG对称,
∴当OP+PC最小时,
由对称性可知,OP+PC=OB.
即OB,AG的交点为点P,
∵∠AOC=60°,OB为菱形OABC的对角线,
∴∠AOB=30°,
∴AP=OAtan30°=2
×
=2,
∴点P的坐标为(2
,2).
(2)连接OB,CD,CQ,BQ,
由(1)知直线AG为抛物线的对称轴,
则四边形ODBC是关于AG成轴对称的图形.
∵点E是OB中点,点F是AB的中点,点P在抛物
线的对称轴上,
∴PE=PF,EF∥OD,CQ=BQ
∠PEF=∠BOA=30°,
即△PEF是底角为30°的等腰三角形.
在△OBC、△BCD中,
OC=BC=BD=2
,∠BOC=∠BDC=30°,
∴△OBC∽△BCD∽△PEF,
∴符合条件的点的坐标为(0,0),(4
,0).
又∵AQ=4,AG=3,BC=2
,
∴GQ=1,BG=
,
∴tan∠GBQ=
=
,
即∠GBQ=30°,
△BQC也是底角为30°的等腰三角形,
∴Q点的(2
,4),
∴符合条件的点M的坐标为(0,0),(4
,0),(2
,4).
 解:(Ⅰ)如图1,作CH⊥OA于点H,
解:(Ⅰ)如图1,作CH⊥OA于点H,四边形OABC是菱形,OA=2
| 3 |
| 3 |
OH=sin60°•2
| 3 |
| 3 |
CH=cos60°•2
| 3 |
A点坐标为(2
| 3 |
C点的坐标为(
| 3 |
由菱形的性质得B点的坐标为(3
| 3 |
设抛物线的解析式为y=ax2+bx+c,根据题意得
|
解得a=-
| 1 |
| 3 |
4
| ||
| 3 |
所以,y=-
| 1 |
| 3 |
4
| ||
| 3 |
(Ⅱ)(1)如图2,由(Ⅰ)知抛物线的解析式为:y=-
| 1 |
| 3 |
4
| ||
| 3 |

即对称轴为x=2
| 3 |
| 3 |
设抛物线与x轴的另一个交点为D,令y=0,得,x2-4
| 3 |
解得x1=0,x2=4
| 3 |
即点D的坐标为(4
| 3 |
∵点A的坐标为(2
| 3 |
| 3 |
且AG⊥BC,
∴直线AG为抛物线的对称轴.
∵B、C两点关于直线AG对称,
∴当OP+PC最小时,
由对称性可知,OP+PC=OB.
即OB,AG的交点为点P,
∵∠AOC=60°,OB为菱形OABC的对角线,
∴∠AOB=30°,
∴AP=OAtan30°=2
| 3 |
| ||
| 3 |
∴点P的坐标为(2
| 3 |
(2)连接OB,CD,CQ,BQ,

由(1)知直线AG为抛物线的对称轴,
则四边形ODBC是关于AG成轴对称的图形.
∵点E是OB中点,点F是AB的中点,点P在抛物
线的对称轴上,
∴PE=PF,EF∥OD,CQ=BQ
∠PEF=∠BOA=30°,
即△PEF是底角为30°的等腰三角形.
在△OBC、△BCD中,
OC=BC=BD=2
| 3 |
∴△OBC∽△BCD∽△PEF,
∴符合条件的点的坐标为(0,0),(4
| 3 |
又∵AQ=4,AG=3,BC=2
| 3 |
∴GQ=1,BG=
| 3 |
∴tan∠GBQ=
| 1 | ||
|
| ||
| 3 |
即∠GBQ=30°,
△BQC也是底角为30°的等腰三角形,
∴Q点的(2
| 3 |
∴符合条件的点M的坐标为(0,0),(4
| 3 |
| 3 |
点评:本题考查了直角三角函数的应用,待定系数法求解析式,菱形的性质,等腰三角形的性质,三角形相似的判定等;连接OB,CD,CQ,BQ,构建相似三角形是本题的关键.

练习册系列答案
相关题目
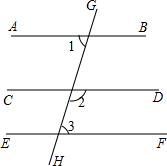 如图,直线AB、CD、EF被直线GH所截,∠1=70°,∠2=110°,∠2+∠3=180°,试说明:(1)EF∥AB.(2)CD∥AB( 补全横线及括号的内容 )
如图,直线AB、CD、EF被直线GH所截,∠1=70°,∠2=110°,∠2+∠3=180°,试说明:(1)EF∥AB.(2)CD∥AB( 补全横线及括号的内容 ) 如图,平行四边形ABCD,E、F为AC上的两点,DE∥BF,求证:AE=CF.
如图,平行四边形ABCD,E、F为AC上的两点,DE∥BF,求证:AE=CF. 如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AB,BD,BC,AC的中点.求证:四边形EFGH是平行四边形.
如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AB,BD,BC,AC的中点.求证:四边形EFGH是平行四边形. 如图,已知AB为⊙O的直径,PB与⊙O相切于点B,线段OP与弦BC垂直并相交于点D,OP与弧BC相交于点E,连接AC.
如图,已知AB为⊙O的直径,PB与⊙O相切于点B,线段OP与弦BC垂直并相交于点D,OP与弧BC相交于点E,连接AC.