题目内容
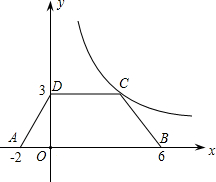 如图,等腰梯形ABCD放置在平面坐标系中,已知A(-2,0)、B(6,0)、D(0,3),反比例函数的图象经过点C.
如图,等腰梯形ABCD放置在平面坐标系中,已知A(-2,0)、B(6,0)、D(0,3),反比例函数的图象经过点C.(1)求点C的坐标和反比例函数的解析式;
(2)若将等腰梯形ABCD向上平移,使平移后的点B落在双曲线上,则应将梯形向上平移几个单位长度?
(3)画出反比例函数在第三象限的草图,若直线AD交双曲线于E,F两点,请求出△EOF的面积.
考点:反比例函数综合题
专题:综合题
分析:(1)过C作CM垂直于x轴,由等腰梯形ABCD,得到AD=BC,OD=CM,利用HL得到直角三角形AOD与直角三角形BMC全等,利用全等三角形对应边相等得到OA=BM,求出OM与CM的长,确定出C坐标,设反比例解析式为y=
(k≠0),将C坐标代入求出k的值,即可确定出反比例解析式;
(2)过B作BN垂直于x轴,与反比例图象交于点N,可得出B与N横坐标相同,将x=6代入反比例解析式求出y的值,即为平移的长度;
(3)画出反比例函数在第三象限图象,如图所示,连接OE,OF,联立直线AD与反比例解析式求出E与F坐标,三角形EOF面积=三角形AOE面积+三角形AOF面积,求出即可.
| k |
| x |
(2)过B作BN垂直于x轴,与反比例图象交于点N,可得出B与N横坐标相同,将x=6代入反比例解析式求出y的值,即为平移的长度;
(3)画出反比例函数在第三象限图象,如图所示,连接OE,OF,联立直线AD与反比例解析式求出E与F坐标,三角形EOF面积=三角形AOE面积+三角形AOF面积,求出即可.
解答: 解:(1)过C作CM⊥x轴,交x轴于点M,可得∠AOD=∠BMC=90°,
解:(1)过C作CM⊥x轴,交x轴于点M,可得∠AOD=∠BMC=90°,
∵等腰梯形ABCD,
∴AD=BC,OD=CM,
在Rt△AOD和Rt△BMC中,
,
∴Rt△AOD≌Rt△BMC(HL),
∴BM=OA=2,CM=OD=3,
∴OM=OB-BM=6-2=4,
∴C(4,3),
设反比例解析式为y=
(k≠0),
将C坐标代入得:k=12,
则反比例解析式为y=
;
(2)过B作BN⊥x轴,与反比例图象交于N点,
将x=6代入y=
得:y=2,
则将等腰梯形ABCD向上平移,使平移后的点B落在双曲线上,则应将梯形向上平移2个单位长度;
(3)如图所示,连接OE,OF,
设直线AD解析式为y=ax+b,
将A(-2,0),D(0,3)代入得:
,
解得:
,
∴直线AD解析式为y=
x+3,
联立得:
,
消去y得:
x+3=
,
整理得:x2+2x-8=0,即(x-2)(x+4)=0,
解得:x=2或x=-4,
将x=2代入得:y=6;将x=-4代入得:y=-3,
∴E(2,6),F(-4,-3),
则S△EOF=S△AOE+S△AOF=
×2×6+
×2×3=6+3=9.
 解:(1)过C作CM⊥x轴,交x轴于点M,可得∠AOD=∠BMC=90°,
解:(1)过C作CM⊥x轴,交x轴于点M,可得∠AOD=∠BMC=90°,∵等腰梯形ABCD,
∴AD=BC,OD=CM,
在Rt△AOD和Rt△BMC中,
|
∴Rt△AOD≌Rt△BMC(HL),
∴BM=OA=2,CM=OD=3,
∴OM=OB-BM=6-2=4,
∴C(4,3),
设反比例解析式为y=
| k |
| x |
将C坐标代入得:k=12,
则反比例解析式为y=
| 12 |
| x |
(2)过B作BN⊥x轴,与反比例图象交于N点,
将x=6代入y=
| 12 |
| x |
则将等腰梯形ABCD向上平移,使平移后的点B落在双曲线上,则应将梯形向上平移2个单位长度;
(3)如图所示,连接OE,OF,
设直线AD解析式为y=ax+b,
将A(-2,0),D(0,3)代入得:
|
解得:
|
∴直线AD解析式为y=
| 3 |
| 2 |
联立得:
|
消去y得:
| 3 |
| 2 |
| 12 |
| x |
整理得:x2+2x-8=0,即(x-2)(x+4)=0,
解得:x=2或x=-4,
将x=2代入得:y=6;将x=-4代入得:y=-3,
∴E(2,6),F(-4,-3),
则S△EOF=S△AOE+S△AOF=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题属于反比例综合题,涉及的知识有:等腰三角形的性质,“HL”证明全等的方法,坐标与图形性质,待定系数法求函数解析式,一次函数与反比例函数的交点,以及三角形面积求法,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
 如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AB,BD,BC,AC的中点.求证:四边形EFGH是平行四边形.
如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AB,BD,BC,AC的中点.求证:四边形EFGH是平行四边形.

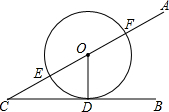 如图,∠ACB=30°,D为CB上一点,CD=
如图,∠ACB=30°,D为CB上一点,CD=