题目内容
抛物线y=x2+bx+c(b,c均为常数)与x轴交于A(1,0),B两点,与y轴交于点C(0,3).
(1)求该抛物线对应的函数表达式;
(2)若P是抛物线上一点,且点P到抛物线的对称轴的距离为3,请直接写出点P的坐标.
(1)求该抛物线对应的函数表达式;
(2)若P是抛物线上一点,且点P到抛物线的对称轴的距离为3,请直接写出点P的坐标.
考点:抛物线与x轴的交点
专题:
分析:(1)抛物线y=x2+bx+c与y轴交于点C(0,3),代入可得出c=3,又由抛物线y=x2+bx+c与x轴交于点A(1,0),代入又可得出b=-4,从而得出抛物线的解析式y=x2-4x+3;
(2)求得对称轴为直线x=2,由点P到抛物线的对称轴的距离为3,可得出点P的横坐标为-1或5,代入抛物线解析式即可得出点P的坐标为(5,8)或(-1,8).
(2)求得对称轴为直线x=2,由点P到抛物线的对称轴的距离为3,可得出点P的横坐标为-1或5,代入抛物线解析式即可得出点P的坐标为(5,8)或(-1,8).
解答:解:(1)∵抛物线y=x2+bx+c与y轴交于点C(0,3),
∴c=3.?
∴y=x2+bx+3.
又∵抛物线y=x2+bx+c与x轴交于点A(1,0),
∴b=-4.?
∴y=x2-4x+3.
(2)点P的坐标为(5,8)或(-1,8).
∴c=3.?
∴y=x2+bx+3.
又∵抛物线y=x2+bx+c与x轴交于点A(1,0),
∴b=-4.?
∴y=x2-4x+3.
(2)点P的坐标为(5,8)或(-1,8).
点评:本题考查了抛物线和x轴的交点问题,以及抛物线的表达式的求法--待定系数法.

练习册系列答案
相关题目
 如图,在△ABC与△BAD中,AD与BC相交于点E,∠C=∠D,EA=EB.
如图,在△ABC与△BAD中,AD与BC相交于点E,∠C=∠D,EA=EB.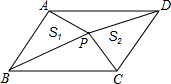 已知:如图,点P为?ABCD内一点,△PAB、△PCD的面积分别记为S1、S2,?ABCD的面积记为S,试探究S1+S2与S之间的关系.
已知:如图,点P为?ABCD内一点,△PAB、△PCD的面积分别记为S1、S2,?ABCD的面积记为S,试探究S1+S2与S之间的关系.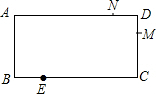 如图,矩形ABCD中,AB=4cm,BC=8cm,动点M从点D出发,按折线DCBAD方向以3cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1cm/s的速度运动,当动点M回到点D时,M、N两点均停止运动.
如图,矩形ABCD中,AB=4cm,BC=8cm,动点M从点D出发,按折线DCBAD方向以3cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1cm/s的速度运动,当动点M回到点D时,M、N两点均停止运动. 已知:如图,点C是线段AB的中点,CE=CD,∠ACD=∠BCE.
已知:如图,点C是线段AB的中点,CE=CD,∠ACD=∠BCE. 如图是一把剪刀的局部示意图,刀片内沿在AB、CD上,EF是刀片外沿.AB、CD相交于点N,EF、CD相交于点M,刀片宽MH=1.5cm.小丽在使用这把剪刀时,∠ANC不超过30°.若想一刀剪断4cm宽的纸带,则刀身AH长至少为
如图是一把剪刀的局部示意图,刀片内沿在AB、CD上,EF是刀片外沿.AB、CD相交于点N,EF、CD相交于点M,刀片宽MH=1.5cm.小丽在使用这把剪刀时,∠ANC不超过30°.若想一刀剪断4cm宽的纸带,则刀身AH长至少为