题目内容
11. 如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE,求证:△ABC≌△DEC.
如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE,求证:△ABC≌△DEC.
分析 由∠BAE=∠BCE=∠ACD=90°,可求得∠DCE=∠ACB,且∠B+∠CEA=∠CEA+∠DEC=180°,可求得∠DEC=∠ABC,再结合条件可证明△ABC≌△DEC.
解答 证明:
∵∠BAE=∠BCE=∠ACD=90°,
∴∠DCE+∠ECA=∠ECA+∠ACB,
∴∠DCE=∠ACB,且∠B+∠CEA=180°,
又∠DEC+∠CEA=180°,
∴∠B=∠DEC,
在△ABC和△DEC中
$\left\{\begin{array}{l}{∠ACB=∠DCE}\\{BC=CE}\\{∠B=∠DEC}\end{array}\right.$
∴△ABC≌△DEC(ASA).
点评 本题主要考查全等三角形的判定,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
6.命题“三角形的内角和等于180°”是( )
| A. | 假命题 | B. | 定义 | C. | 定理 | D. | 基本事实 |
1.若菱形的周长为52cm,面积为120cm2,则它的对角线之和为( )
| A. | 14cm | B. | 17cm | C. | 28cm | D. | 34cm |
 将长方形纸片ABCD沿AE折叠,点D落在长方形内的点处,如图所示,已知∠CED′=70°,则∠AED等于55度.
将长方形纸片ABCD沿AE折叠,点D落在长方形内的点处,如图所示,已知∠CED′=70°,则∠AED等于55度.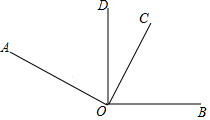 如图,已知∠AOB=155°,∠AOC=∠BOD=90°.
如图,已知∠AOB=155°,∠AOC=∠BOD=90°.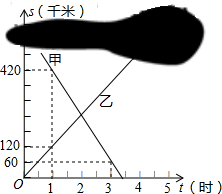 甲、乙两列火车分别从A、B两城同时匀速驶出,甲车开往B城,乙车开往A城.由于墨迹遮盖,图中提供的是两车距B城的路程S甲(千米)、S乙(千米)与行驶时间t(时)的函数图象的一部分.
甲、乙两列火车分别从A、B两城同时匀速驶出,甲车开往B城,乙车开往A城.由于墨迹遮盖,图中提供的是两车距B城的路程S甲(千米)、S乙(千米)与行驶时间t(时)的函数图象的一部分.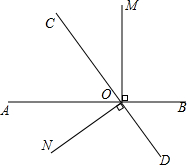 如图,直线AB、CD相交于点O,∠BOM=90°,∠DON=90°.
如图,直线AB、CD相交于点O,∠BOM=90°,∠DON=90°.