题目内容
16.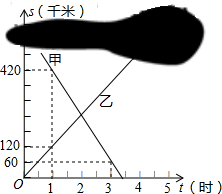 甲、乙两列火车分别从A、B两城同时匀速驶出,甲车开往B城,乙车开往A城.由于墨迹遮盖,图中提供的是两车距B城的路程S甲(千米)、S乙(千米)与行驶时间t(时)的函数图象的一部分.
甲、乙两列火车分别从A、B两城同时匀速驶出,甲车开往B城,乙车开往A城.由于墨迹遮盖,图中提供的是两车距B城的路程S甲(千米)、S乙(千米)与行驶时间t(时)的函数图象的一部分.(1)分别求出S甲、S乙与t的函数关系式(不必写出t的取值范围);
(2)求A、B两城之间的距离,及t为何值时两车相遇;
(3)当两车相距300千米时,求t的值.
分析 (1)根据函数图象可以分别求得S甲、S乙与t的函数关系式;
(2)将t=0代入S甲=-180t+600,即可求得A、B两城之间的距离,然后将(1)中的两个函数相等,即可求得t为何值时两车相遇;
(3)根据题意可以列出相应的方程,从而可以求得t的值.
解答 解:(1)设S甲与t的函数关系式是S甲=kt+b,
$\left\{\begin{array}{l}{k+t=420}\\{3k+t=60}\end{array}\right.$,得$\left\{\begin{array}{l}{k=-180}\\{t=600}\end{array}\right.$,
即S甲与t的函数关系式是S甲=-180t+600,
设S乙与t的函数关系式是S甲=at,
则120=a×1,得a=120,
即S乙与t的函数关系式是S甲=120t;
(2)将t=0代入S甲=-180t+600,得
S甲=-180×0+600,得S甲=600,
令-180t+600=120t,
解得,t=2,
即A、B两城之间的距离是600千米,t为2时两车相遇;
(3)由题意可得,
|-180t+600-120t|=300,
解得,t1=1,t3=3,
即当两车相距300千米时,t的值是1或3.
点评 本题考查一次函数的应用,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.下列图案中,是轴对称图形且有两条对称轴的是( )
| A. |  | B. |  | C. |  | D. |  |
1. 如图所示,能读出的线段条数共有( )
如图所示,能读出的线段条数共有( )
 如图所示,能读出的线段条数共有( )
如图所示,能读出的线段条数共有( )| A. | 8条 | B. | 10条 | C. | 6条 | D. | 12条 |
8.若等腰三角形的周长为28cm,一边为10cm,则腰长为( )
| A. | 10cm | B. | 9cm | C. | 10cm或9cm | D. | 8cm |
5.下列计算结果正确的是( )
| A. | -(2x-y)=-2x-y | B. | -3a+(4a2+2)=-3a+4a2-2 | ||
| C. | -(2a-3y)=-2a+3y | D. | -3(a-7)=-3a+7 |
 如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE,求证:△ABC≌△DEC.
如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE,求证:△ABC≌△DEC.