题目内容
1.若菱形的周长为52cm,面积为120cm2,则它的对角线之和为( )| A. | 14cm | B. | 17cm | C. | 28cm | D. | 34cm |
分析 作出图形,根据菱形的对角线互相垂直平分可得AC⊥BD,AO=CO=$\frac{1}{2}$AC,BO=DO=$\frac{1}{2}$BD,然后根据菱形的面积等于对角线乘积的一半列式整理可得AO•BO=60,根据菱形的周长求出AB=13,再利用勾股定理可得AO2+BO2=169,然后利用完全平方公式整理并求出AO+BO,再求解即可.
解答 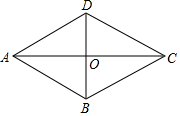 解:如图,∵四边形ABCD是菱形,
解:如图,∵四边形ABCD是菱形,
∴AC⊥BD,AO=CO=$\frac{1}{2}$AC,BO=DO=$\frac{1}{2}$BD,
∵菱形的面积为120cm2,
∴$\frac{1}{2}$AC•BD=120,
即$\frac{1}{2}$×2AO•2BO=120,
所以,AO•BO=60,
∵菱形的周长为52cm,
∴AB=13cm,
在Rt△AOB中,由勾股定理得,AO2+BO2=AB2=132=169,
所以,(AO+BO)2=AO2+2AO•BO+BO2=169+60×2=289,
所以,AO+BO=17,
所以,AC+BD=2(AO+BO)=2×17=34cm.
故选D.
点评 本题考查了菱形的性质,勾股定理,完全平方公式,熟练掌握菱形的性质是解题的关键,作出图形更形象直观.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
16.已知a-b=5,ab=-2,则代数式a2+b2-1的值是( )
| A. | 16 | B. | 18 | C. | 20 | D. | 28 |
13.$\sqrt{2}$tan45°的值为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
10.若关于x的方程$\frac{3-2x}{x-3}$+$\frac{2+mx}{3-x}$=-1无解,则m的值为( )
| A. | 3 | B. | -3 | C. | -$\frac{5}{3}$ | D. | 0 |
11.有理数-32,(-3)2,|-33|按从小到大的顺序排列是( )
| A. | |-33|<-32<(-3)2 | B. | |-33|<(-3)2<-32 | C. | -32<|-33|<(-3)2 | D. | -32<(-3)2<|-33| |
 如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE,求证:△ABC≌△DEC.
如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE,求证:△ABC≌△DEC.