题目内容
13．
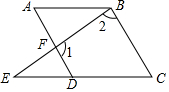如图，已知∠A=∠C，∠1与∠2互补，求证：AB∥CD．要求：写出推理步骤和每一步的推理依据．
分析 先根据同旁内角互补，两直线平行，判定AD∥BC，再根据两直线平行，同旁内角互补，得出∠C+∠ADC=180°，再根据∠A=∠C即可得到∠A+∠ADC=180°，即可判定AB∥CD．
解答 证明：∵∠1与∠2互补（已知），
∴AD∥BC（同旁内角互补，两直线平行），
∴∠C+∠ADC=180°（两直线平行，同旁内角互补），
又∵∠A=∠C（已知），
∴∠A+∠ADC=180°（等量代换），
∴AB∥CD（同旁内角互补，两直线平行）．
点评 本题主要考查了平行线的性质与判定的运用，解题时注意：同旁内角互补，两直线平行；两直线平行，同旁内角互补．
练习册系列答案
相关题目
8．
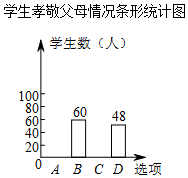某校为了了解学生孝敬父母的情况（选项：A．为父母洗一次脚；B．帮父母做一次家务；C．给父母买一件礼物；D．其它），在全校范围内随机抽取了若干名学生进行调查，得到如图表（部分信息未给出）：根据以上信息解答下列问题：
学生孝敬父母情况统计表：
（1）表中m=36，n=96，p=0.25．
（2）这次被调查的学生有多少人？并补全条形统计图．
（3）该校有1600名学生，估计该校全体学生中选择B选项的有多少人？
某校为了了解学生孝敬父母的情况（选项：A．为父母洗一次脚；B．帮父母做一次家务；C．给父母买一件礼物；D．其它），在全校范围内随机抽取了若干名学生进行调查，得到如图表（部分信息未给出）：根据以上信息解答下列问题：学生孝敬父母情况统计表：
| 选项 | 频数 | 频率 |
| A | m | 0.15 |
| B | 60 | p |
| C | n | 0.4 |
| D | 48 | 0.2 |
（2）这次被调查的学生有多少人？并补全条形统计图．
（3）该校有1600名学生，估计该校全体学生中选择B选项的有多少人？
已知：抛物线y=ax2+bx-3经过点A（7，-3），与x轴正半轴交于点B（m，0）、C（6m、0）两点，与y轴交于点D．