题目内容
1.你能化简 (a-1)(a99+a98+a97+…+a2+a+1)吗?我们不妨先从简单情况入手,发现规律,归纳结论.
(1)先填空:(a-1)(a+1)=a2-1;(a-1)(a2+a+1)=a3-1;(a-1)(a3+a2+a+1)=a4-1;…
由此猜想:(a-1)(a99+a98+a97+…+a2+a+1)=a100-1
(2)利用这个结论,你能解决下面两个问题吗?
①求 2199+2198+2197+…+22+2+1 的值;
②若 a5+a4+a3+a2+a+1=0,则a6等于多少?
分析 (1)利用多项式乘以多项式法则计算得到结果,归纳总结得到一般性规律,即可确定出结果;
(2)利用得出的结果将原式变形,计算即可得到结果.
解答 解:(1)a2-1;a3-1;a4-1;a100-1;
故答案为:a2-1;a3-1;a4-1;a100-1;
(2)①(2-1)(299+298+297+…+22+2+1)=2100-1,由于2-1=1,
则299+298+297+…+22+2+1=2100-1;
②∵a6-1=(a-1)(a5+a4+a3+a2+a+1)=0,
∴a6=1,
∴a=±1,
但当a=1时,a5+a4+a3+a2+a+1=0不成立,
则a=-1.
点评 此题考查了平方差公式,以及规律型:数字的变化类,弄清题中的规律是解本题的关键.

练习册系列答案
相关题目
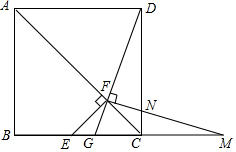 如图.在正方形ABCD中,点E是BC边上的中点,EF⊥AC于点F.连接DF并延长交BC于G.过F作FM⊥DG交CD于N,交BC的延长线于点M.
如图.在正方形ABCD中,点E是BC边上的中点,EF⊥AC于点F.连接DF并延长交BC于G.过F作FM⊥DG交CD于N,交BC的延长线于点M. 如图所示,AB⊥l1,AC⊥l2,则点A到直线l1的距离是线段AB的长度.
如图所示,AB⊥l1,AC⊥l2,则点A到直线l1的距离是线段AB的长度.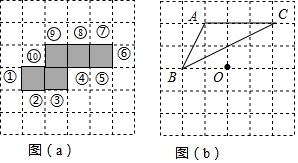
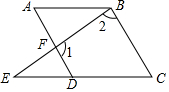 如图,已知∠A=∠C,∠1与∠2互补,求证:AB∥CD.
如图,已知∠A=∠C,∠1与∠2互补,求证:AB∥CD. 如图,Rt△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿AD折叠,使AC落在斜边AB上且与AE重合,则CD=3.
如图,Rt△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿AD折叠,使AC落在斜边AB上且与AE重合,则CD=3.