题目内容
18.在△ABC中,已知BC=4cm,以边AC的中点P为圆心1cm为半径画⊙P,以边AB的中点Q为圆心x cm长为半径画⊙Q,如果⊙P与⊙Q相切,那么x=1或3cm.分析 根据三角形的中位线的性质得到PQ=$\frac{1}{2}$BC=2cm,①当⊙P与⊙Q相外切时,②当⊙P与⊙Q相内切时,列方程即可得到结论.
解答 解:∵BC=4cm,点P是AC的中点,点Q是AB的中点,
∴PQ=$\frac{1}{2}$BC=2cm,
①当⊙P与⊙Q相外切时,PQ=1+x=2,
∴x=1cm,
②当⊙P与⊙Q相内切时,PQ=|x-1|=2,
∴x=3cm(负值舍去),
∴如果⊙P与⊙Q相切,那么x=1cm或3cm,
故答案为:1或3.
点评 本题考查了相切两圆的性质,三角形的中位线的性质,注意相切两圆的两种情况.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.某电器超市销售每台进价分别为400元、340元的A、B两种型号的豆浆机.下表是近两周的销售情况:
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)第三周该超市采购这两种型号的豆浆机共20台,如果全部售出,要使销售利润不少于1600元,求至少购进A种型号豆浆机多少台?
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一周 | 3台 | 5台 | 3500 |
| 第二周 | 4台 | 10台 | 6000 |
(1)求A、B两种型号的电风扇的销售单价;
(2)第三周该超市采购这两种型号的豆浆机共20台,如果全部售出,要使销售利润不少于1600元,求至少购进A种型号豆浆机多少台?
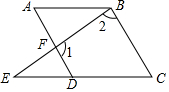 如图,已知∠A=∠C,∠1与∠2互补,求证:AB∥CD.
如图,已知∠A=∠C,∠1与∠2互补,求证:AB∥CD.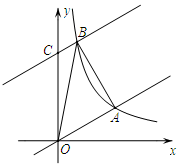 如图,在平面直角坐标系xOy中,直线y=$\frac{\sqrt{3}}{3}$x与反比例函数y=$\frac{k}{x}$在第一象限内的图象相交于点A(m,3).
如图,在平面直角坐标系xOy中,直线y=$\frac{\sqrt{3}}{3}$x与反比例函数y=$\frac{k}{x}$在第一象限内的图象相交于点A(m,3).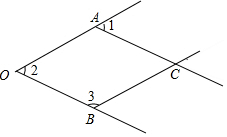 如图所示的是一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.(将下列解答过程补充完整)
如图所示的是一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.(将下列解答过程补充完整)