题目内容
13.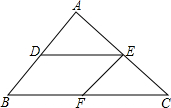 如图,已知DE∥BC,EF∥AB,则下列比例式中错误的是( )
如图,已知DE∥BC,EF∥AB,则下列比例式中错误的是( )| A. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | B. | $\frac{CE}{CF}$=$\frac{EA}{FB}$ | C. | $\frac{DE}{BC}$=$\frac{AD}{BD}$ | D. | $\frac{EF}{AB}$=$\frac{CF}{CB}$ |
分析 根据平行线分线段成比例定理由DE∥BC可判断$\frac{AD}{AB}$=$\frac{AE}{AC}$,$\frac{AD}{AB}$=$\frac{DE}{BC}$,则可对A、C进行判断,由EF∥AB得到$\frac{CE}{AE}$=$\frac{CF}{BF}$,$\frac{EF}{AB}$=$\frac{CF}{CB}$,可对B、D进行判断.
解答 解:A、∵DE∥BC,∴$\frac{AD}{AB}$=$\frac{AE}{AC}$,所以A选项的比例式正确;
B、∵EF∥AB,∴$\frac{CE}{AE}$=$\frac{CF}{BF}$,即$\frac{CE}{CF}$=$\frac{AE}{BF}$,所以B选项的比例式正确;
C、∵DE∥BC,∴$\frac{AD}{AB}$=$\frac{DE}{BC}$,所以C选项的比例式错误;
D、∵EF∥AB,∴$\frac{EF}{AB}$=$\frac{CF}{CB}$,即$\frac{CE}{CF}$=$\frac{AE}{BF}$,所以D选项的比例式错误.
故选C.
点评 本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 如图.已知⊙O中,△OMN是等腰三角形OB、OC分别交AC、DB于点M,N,求证:$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$.
如图.已知⊙O中,△OMN是等腰三角形OB、OC分别交AC、DB于点M,N,求证:$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$. 如图,在△ABC中,D、E分别为AB、CA的中点,连接DE、BE、CD,BE与CD交于点F,求$\frac{DF}{FC}$的值.
如图,在△ABC中,D、E分别为AB、CA的中点,连接DE、BE、CD,BE与CD交于点F,求$\frac{DF}{FC}$的值.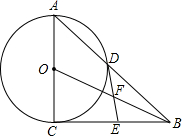 如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交斜边于点D,点E为BC上一点,BE=DE,连接OB交DE于点F.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交斜边于点D,点E为BC上一点,BE=DE,连接OB交DE于点F.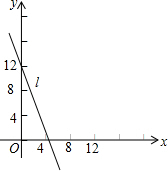 如图,直线l是一次函数y=kx+b的图象,观察图象可知:
如图,直线l是一次函数y=kx+b的图象,观察图象可知: 我们知道,对于一些立体图形问题,常把它转化为平面图形来研究和处理,棱长为a的正方体摆成如图所示的形状,问:
我们知道,对于一些立体图形问题,常把它转化为平面图形来研究和处理,棱长为a的正方体摆成如图所示的形状,问: