题目内容
5.设x1,x2是方程x2-x-912=0的两个实数根,则${x}_{1}^{3}$+912x2-912=913.分析 先根据一元二次方程的解的定义得到x12=x1+912,再计算x13=x12+912x1=913x1+912,则原式可化简为913(x1+x2),然后利用根与系数的关系求解.
解答 解:∵x1是方程x2-x-912=0的两实数根,
∴x12=x1+912,
∴x13=x12+912x1=x1+912+912x1=913x1+912,
∴原式=913x1+912+913x2-912=913(x1+x2),
∵x1,x2是方程x2-x-912=0的两实数根,
∴x1+x2=1,
∴原式=913.
故答案为:913.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
13.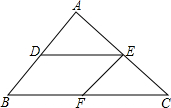 如图,已知DE∥BC,EF∥AB,则下列比例式中错误的是( )
如图,已知DE∥BC,EF∥AB,则下列比例式中错误的是( )
 如图,已知DE∥BC,EF∥AB,则下列比例式中错误的是( )
如图,已知DE∥BC,EF∥AB,则下列比例式中错误的是( )| A. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | B. | $\frac{CE}{CF}$=$\frac{EA}{FB}$ | C. | $\frac{DE}{BC}$=$\frac{AD}{BD}$ | D. | $\frac{EF}{AB}$=$\frac{CF}{CB}$ |
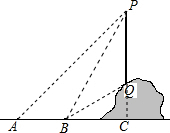 如图所示,从地面上一点A测出山顶电视塔的上端P点的仰角是45°,向前走60米到B点测得P点的仰角是60°,电视塔底部Q的仰角是30°,求电视塔PQ的高度(精确到1米)
如图所示,从地面上一点A测出山顶电视塔的上端P点的仰角是45°,向前走60米到B点测得P点的仰角是60°,电视塔底部Q的仰角是30°,求电视塔PQ的高度(精确到1米)