题目内容
3. 如图.已知⊙O中,△OMN是等腰三角形OB、OC分别交AC、DB于点M,N,求证:$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$.
如图.已知⊙O中,△OMN是等腰三角形OB、OC分别交AC、DB于点M,N,求证:$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$.
分析 由SAS证明△OBN≌△OCM,得出∠BNO=∠CMO,∠OBN=∠OCM,再由等腰三角形的性质证出∠ACB=∠DBC,由圆周角定理得出$\widehat{AB}=\widehat{CD}$,连接BC,证出MN∥BC,作OE⊥BC于E,则O、F、E三点共线,得出F为△OBC三条高的交点,因此OM⊥AC,由垂径定理得出$\widehat{AB}=\widehat{BC}$,即可得出结论.
解答 证明:∵△OMN是等腰三角形,
∴OM=ON,
在△OBN和△OCM中,
$\left\{\begin{array}{l}{OB=OC}&{\;}\\{∠O=∠O}&{\;}\\{ON=OM}&{\;}\end{array}\right.$,
∴△OBN≌△OCM(SAS),
∴∠BNO=∠CMO,∠OBN=∠OCM,
∵OA=OB,
∴∠OBC=∠OCB,
∴∠ACB=∠DBC,
∴$\widehat{AB}=\widehat{CD}$,
连接BC,如图所示:
∵OM=ON,OB=OC,
∴OM:OB=ON:OC,
∴MN∥BC,
作OE⊥BC于E,则O、F、E三点共线,
∵OB=OC,OE⊥BC,
∴F为△OBC三条高的交点,
∴OM⊥AC,
∴$\widehat{AB}=\widehat{BC}$,
∴$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$.
点评 本题考查了全等三角形的判定与性质、等腰三角形的性质、圆周角定理、垂径定理、平行线的判定等知识;本题综合性强,有一定难度,需要通过作辅助线才能得出结论.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
14.已知函数y=(m-1)xm2+m-2是x的一次函数,则常数m的值为( )
| A. | -1 | B. | 1或-1 | C. | 1 | D. | 2或-1 |
13.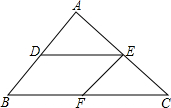 如图,已知DE∥BC,EF∥AB,则下列比例式中错误的是( )
如图,已知DE∥BC,EF∥AB,则下列比例式中错误的是( )
 如图,已知DE∥BC,EF∥AB,则下列比例式中错误的是( )
如图,已知DE∥BC,EF∥AB,则下列比例式中错误的是( )| A. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | B. | $\frac{CE}{CF}$=$\frac{EA}{FB}$ | C. | $\frac{DE}{BC}$=$\frac{AD}{BD}$ | D. | $\frac{EF}{AB}$=$\frac{CF}{CB}$ |
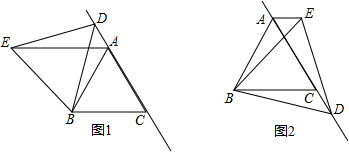
 如图,反比例函数y=$\frac{8}{x}$(x>0)的图象分别与正比例函数y=2x,y=$\frac{1}{2}$x的图象交于A、B两点.求△OAB的面积.
如图,反比例函数y=$\frac{8}{x}$(x>0)的图象分别与正比例函数y=2x,y=$\frac{1}{2}$x的图象交于A、B两点.求△OAB的面积.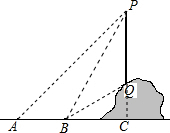 如图所示,从地面上一点A测出山顶电视塔的上端P点的仰角是45°,向前走60米到B点测得P点的仰角是60°,电视塔底部Q的仰角是30°,求电视塔PQ的高度(精确到1米)
如图所示,从地面上一点A测出山顶电视塔的上端P点的仰角是45°,向前走60米到B点测得P点的仰角是60°,电视塔底部Q的仰角是30°,求电视塔PQ的高度(精确到1米) 已知:如图,AB为⊙O的直径,∠ABT=45°,AT=AB,求证:AT与⊙O相切.
已知:如图,AB为⊙O的直径,∠ABT=45°,AT=AB,求证:AT与⊙O相切.