题目内容
13.下列关于x的方程中,一定有实数解的是( )| A. | $\sqrt{x-1}=-1$ | B. | $\sqrt{x-1}=x$ | C. | x2+mx-1=0 | D. | $\frac{x}{x-1}=\frac{1}{x-1}$ |
分析 先解答选项中的各个方程,即可判断那个选项中的方程一定有实数解,从而可以解答本题.
解答 解:∵$\sqrt{x-1}≥0$,∴$\sqrt{x-1}=-1$无解,故选项A错误;
∵$\sqrt{x-1}=x$,得x-1=x2,∴x2-x+1=0,则△=(-1)2-4×1×1=1-4=-3<0,故此方程无解,故选项B错误;
∵x2+mx-1=0,∴△=m2-4×1×(-1)=m2+4>0,∴x2+mx-1=0一定有两个不相等的实数根,故选项C正确;
∵$\frac{x}{x-1}=\frac{1}{x-1}$,解得,x=1,而x=1时,x-1=0,故此分式方程无解,故选项D错误;
故选C.
点评 本题考查无理方程、根的判别式、分式方程的解,解题的关键是明确无理方程根号里面的数或式子大于等于0,根的判别式△≥0时,方程有实数根,分式方程的解要使得原分式方程有意义.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
2.下列结论中正确的是( )
| A. | 正数、负数统称为有理数 | B. | 无限小数都是无理数 | ||
| C. | 有理数、无理数统称为实数 | D. | 两个无理数的和一定是无理数 |
 如图,点P是等腰Rt△ABC底边BC上一点,过点P作BA、AC的垂线,垂足为E、F,设点D为BC中点,求证:△DEF是等腰直角三角形.
如图,点P是等腰Rt△ABC底边BC上一点,过点P作BA、AC的垂线,垂足为E、F,设点D为BC中点,求证:△DEF是等腰直角三角形.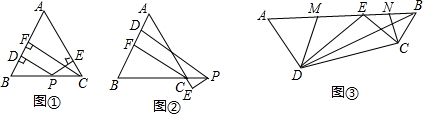
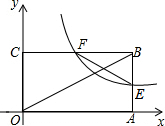 如图,矩形OABC中,OB=6,点O是坐标原点,点A,C分别在x轴,y轴的正半轴上,反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象分别交AB,BC于点E,F,F是BC的中点,则EF的长为3.
如图,矩形OABC中,OB=6,点O是坐标原点,点A,C分别在x轴,y轴的正半轴上,反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象分别交AB,BC于点E,F,F是BC的中点,则EF的长为3.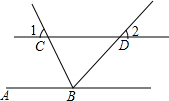 如图,直线AB∥CD,BC平分∠ABD,∠1=67°,则∠2=46度.
如图,直线AB∥CD,BC平分∠ABD,∠1=67°,则∠2=46度.