题目内容
8.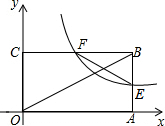 如图,矩形OABC中,OB=6,点O是坐标原点,点A,C分别在x轴,y轴的正半轴上,反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象分别交AB,BC于点E,F,F是BC的中点,则EF的长为3.
如图,矩形OABC中,OB=6,点O是坐标原点,点A,C分别在x轴,y轴的正半轴上,反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象分别交AB,BC于点E,F,F是BC的中点,则EF的长为3.
分析 连接AC,根据矩形的性质得到AC=BO=6,根据反比例函数图象上点的坐标特征求出点E是AB的中点,根据三角形中位线定理计算即可.
解答 解:连接AC,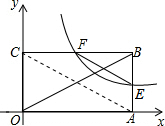
∵四边形OABC是矩形,
∴AC=BO=6,
设OA=a,OC=b,
则CF=$\frac{a}{2}$,
∵点F在反比例函数y=$\frac{k}{x}$的图象上,
∴$\frac{1}{2}$ab=k,
设点E的坐标为(a,d),
∵点E在反比例函数y=$\frac{k}{x}$的图象上,
∴ad=k=$\frac{1}{2}$ab,
∴d=$\frac{1}{2}$b,即点E是AB的中点,
∴EF=$\frac{1}{2}$AC=3,
故答案为:3.
点评 本题考查的是反比例函数图象上点的坐标特征、矩形的性质和三角形中位线定理的应用,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
13.下列关于x的方程中,一定有实数解的是( )
| A. | $\sqrt{x-1}=-1$ | B. | $\sqrt{x-1}=x$ | C. | x2+mx-1=0 | D. | $\frac{x}{x-1}=\frac{1}{x-1}$ |
17.下列运算正确的是( )
| A. | 3a+2a=5a2 | B. | (2a)3=6a3 | C. | (x+1)2=x2+1 | D. | (x+2)(x-2)=x2-4 |
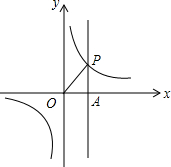 如图,函数y=$\frac{k}{x}$的图象与直线x=2交于第一象限的点P,△AOP的面积等于$\frac{1}{2}$.
如图,函数y=$\frac{k}{x}$的图象与直线x=2交于第一象限的点P,△AOP的面积等于$\frac{1}{2}$.
 如图,AB是半⊙O的直径,点C在半⊙O上,∠B=∠DCA,AD∥BC,连结OD、AC.
如图,AB是半⊙O的直径,点C在半⊙O上,∠B=∠DCA,AD∥BC,连结OD、AC.