题目内容
13.端午节前夕,某蛋糕房推出有A、B、C、D四种口味的粽子,为调查市民对这四种口味的喜爱情况,随机做了问卷调查,并将调查情况全部回收后绘制成如下两幅统计图(尚不完整)
请根据以上信息回答:
(1)本次随机发放了600份调查问卷;
(2)请将上述两幅不完整的统计图补充完整;
(3)若该学校共有2000人,请问喜欢A种口味粽子大约有多少人?
(4)若某人4种口味的粽子各买1个,它们的外包装完全一样,煮熟后他先后随机品尝了2个,请用列表或画树状图的方式,求他第2个品尝到A种口味粽子的概率.
分析 (1)用B类的人数除以它所占的百分比即可得到调查问卷的总份数;
(2)先计算出C类人数,再分别计算出C类和A类所占的百分比,然后补全统计图;
(3)利用样本估计总体,用样本中喜欢A种口味粽子所占的百分比乘以2000即可;
(4)画树状图展示所有12种等可能的结果数,再找出第2个品尝到A种口味粽子的结果数,然后根据概率公式求解.
解答 解:(1)本次随机发放的调查问卷总数为:60÷10%=600(份);
故答案为600;
(2)C类人数=600-180-60-240=120,
C类所占的百分比=$\frac{120}{600}$×100%=20%,
A类所占的百分比=$\frac{240}{600}$×100%=40%,
如图,
(3)2000×30%=600,
所以估计喜欢A种口味粽子大约有600人;
(4)画树状图为:
共有12种等可能的结果数,其中第2个品尝到A种口味粽子的结果数为3,
所以第2个品尝到A种口味粽子的概率=$\frac{3}{12}$=$\frac{1}{4}$.
点评 本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查了统计图.

练习册系列答案
相关题目
4. 随着智能手机的普及,QQ、微博、微信等新型社交平台的兴起,在公共场所的“低头族”越来越多,针对“您如何人看待低头族”的问题,晨光数学小组在全校范围内进行了随机调查,发放了调查问卷,并将调查结果绘制成了如图所示的统计图表(均不完整).
随着智能手机的普及,QQ、微博、微信等新型社交平台的兴起,在公共场所的“低头族”越来越多,针对“您如何人看待低头族”的问题,晨光数学小组在全校范围内进行了随机调查,发放了调查问卷,并将调查结果绘制成了如图所示的统计图表(均不完整).
请根据统计图中提供的信息,解答下列问题:
(1)本次接受调查的总人数是200人;
(2)通过计算,将条形统计图补充完整;
(3)扇形统计图中,观点“D”的百分比是24%,“B”所对应的圆心角的度数是126°;
(4)估算在全校3000名学生中,对“低头族”表示不赞同的人数.
 随着智能手机的普及,QQ、微博、微信等新型社交平台的兴起,在公共场所的“低头族”越来越多,针对“您如何人看待低头族”的问题,晨光数学小组在全校范围内进行了随机调查,发放了调查问卷,并将调查结果绘制成了如图所示的统计图表(均不完整).
随着智能手机的普及,QQ、微博、微信等新型社交平台的兴起,在公共场所的“低头族”越来越多,针对“您如何人看待低头族”的问题,晨光数学小组在全校范围内进行了随机调查,发放了调查问卷,并将调查结果绘制成了如图所示的统计图表(均不完整).| 您如何看待“低头族”的调查问卷 您好!这是一份关于您如何看待低头族的问卷调查表,请在表格内选择一项您最认同的观点,在其后的空格内打对勾,感谢您的参与! | ||
| 代码 | 观点 | 您的选择 |
| A | 获取信息方便 | |
| B | 联系朋友方便 | |
| C | 对视力不好,影响健康 | |
| D | 使朋友亲人疏远,不利于交流 | |
(1)本次接受调查的总人数是200人;
(2)通过计算,将条形统计图补充完整;
(3)扇形统计图中,观点“D”的百分比是24%,“B”所对应的圆心角的度数是126°;
(4)估算在全校3000名学生中,对“低头族”表示不赞同的人数.
1.下列命题是假命题的是( )
| A. | 两个角的和等于平角时,这两个角互为补角 | |
| B. | 平行于同一直线的两直线平行 | |
| C. | 垂直于同一直线的两直线平行 | |
| D. | 如果$\frac{a}{c}$=$\frac{b}{c}$那么a=b |
8.若m是任意实数,则点M(m2+2,-2)在第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
3. 如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点一次用A1,A2,A3,A4,…表示,则顶点A2016的坐标是( )
如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点一次用A1,A2,A3,A4,…表示,则顶点A2016的坐标是( )
 如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点一次用A1,A2,A3,A4,…表示,则顶点A2016的坐标是( )
如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点一次用A1,A2,A3,A4,…表示,则顶点A2016的坐标是( )| A. | (504,504) | B. | (-504,504) | C. | (-504,-504) | D. | (504,-504) |
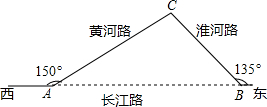 如图,已知:长江路西段与黄河路的夹角为150°,长江路东段与淮河路的夹角为135°,黄河路全长AC=20km,从A地道B地必须先走黄河路经C点后再走淮河路才能到达,城市道路改造后,直接打通长江路(即修建AB路段).问:打通长江路后从A地道B地可少走多少路程?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
如图,已知:长江路西段与黄河路的夹角为150°,长江路东段与淮河路的夹角为135°,黄河路全长AC=20km,从A地道B地必须先走黄河路经C点后再走淮河路才能到达,城市道路改造后,直接打通长江路(即修建AB路段).问:打通长江路后从A地道B地可少走多少路程?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7) 某教学学习小组对“人们了解国家大事的途径”进行调查.
某教学学习小组对“人们了解国家大事的途径”进行调查.