Question

19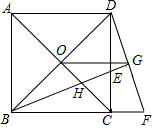．如图，点O是正方形ABCD的对角线交点，BE平分∠DBC，交DC于点E，交AC于H，延长BC到点F，使CF=CE，连结DF，交BE的延长线于点G，连结OG，下列四个结论：①BG⊥DF；②OG∥AD；③BH=GH；④若正方形ABCD的边长是1，则CE=$\sqrt{2}$-1．其中正确的结论有①②④（把你认为正确结论的序号都填上）．

Answer 1

分析 ①根据正方形的性质可以得到∠DCF=90°=∠BCD，根据SAS即可证得△BCE≌△DCF，得出∠1=∠F，∠F+∠2=90°，进而得出∠BGD=90°=∠BGF；
②根据全等三角形的性质得到∠CBE=∠CDF，于是得到∠DGB=∠BCE=90°，根据三角形中位线的性质即可得到结论；
③由C不是BF中点，得到OC与DF不平行，由于O为BD中点，于是得到BH≠GH，故③错误；
④过E作EH⊥BD于H，于是得到△DHE是等腰直角三角形，根据等腰直角三角形的性质得到DH=HE，根据角平分线的性质得到HE=CE，根据全等三角形的性质得到BH=BC=1，于是得到CE=HE=DE=$\sqrt{2}$-1，故④正确，

解答 解：①∵正方形ABCD中，BC=DC，∠BCD=90°，
∴∠BCD=∠DCF=90°，
∴∠DCF=90°=∠BCD，
∵在△BCD和△DCF中，
$\left\{\begin{array}{l}{BC=DC}\\{∠BCD=∠DCF}\\{CE=CF}\end{array}\right.$，
∴△BCE≌△DCF（SAS），
∴∠1=∠F，
∵∠BCD=90°，
∴∠1+∠2=90°，
∴∠F+∠2=90°，
∵D、G、F三点共线，
∴∠BGF+∠BGD=180°，
∴∠BGD=90°=∠BGF，
即BG⊥DF；故①正确；
②∵△BCE≌△DCF，
∴∠CBE=∠CDF，
∵∠BEC=∠DEG，
∴∠DGB=∠BCE=90°，
∴BG垂直且平分DF，
∵O是BD的中点，
∴OG∥BF，
∴OG∥AD．
故②选项正确；
③∵C不是BF中点，
∴OC与DF不平行，
而O为BD中点，
∴BH≠GH，故③错误；
④过E作EH⊥BD于H，
则△DHE是等腰直角三角形，
∴DH=HE，
∵BE平分∠DBC，
∴HE=CE，
在Rt△BCE与Rt△BHE中，$\left\{\begin{array}{l}{CE=HE}\\{BE=BE}\end{array}\right.$，
∴Rt△BCE≌Rt△BHE，
∴BH=BC=1，
∵BD=$\sqrt{2}$BC=$\sqrt{2}$，
∴CE=HE=DE=$\sqrt{2}$-1，故④正确，
故答案为：①②④．

点评 本题主要考查了正方形的性质，涉及全等三角形的判定与性质及正方形的性质，解题的关键是灵活运用三角形全等的判定及性质．