题目内容
10.若关于x、y的二元一次方程组$\left\{\begin{array}{l}{3x+y=1+a①}\\{x+3y=3②}\end{array}\right.$的解满足0<x+y<2,求a的取值范围.分析 直接把方程组的两个方程相加表示出x+y,再根据0<x+y<2,得到关于a的不等式组,解出即可.
解答 解:①+②,得:4x+4y=4+a,
则x+y=$\frac{a+4}{4}$,
由0<x+y<2得0<$\frac{a+4}{4}$<2,
解之可得:-4<a<4,
故答案为:-4<a<4.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程成立的未知数的值.

练习册系列答案
相关题目
18.用每分可抽30t水的抽水机来抽污水管道内的污水,估计积存的污水超过1200t而不足1500t,则将污水抽完所用时间x的取值范围是( )
| A. | 40<x≤50 | B. | 40≤x<50 | C. | 40<x<50 | D. | 40≤x≤50 |
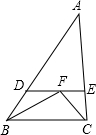 如图,在△ABC中,已知∠ABC和∠ACB的平分线交于点F,过F作DE∥BC,交AB于点D,交AC于点E,若BD+CE=10,则线段DE的长为10.
如图,在△ABC中,已知∠ABC和∠ACB的平分线交于点F,过F作DE∥BC,交AB于点D,交AC于点E,若BD+CE=10,则线段DE的长为10. 用4块相同的立方体搭成的几何体的主视图如图所示.
用4块相同的立方体搭成的几何体的主视图如图所示.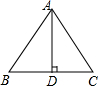 如图,在△ABC中,AB=AC=5cm,BC=6cm,AD平分∠BAC,则AD=4cm.
如图,在△ABC中,AB=AC=5cm,BC=6cm,AD平分∠BAC,则AD=4cm. 如图,AC平分∠BAD,∠1=∠2,那么AB=AD成立吗?请说明理由.
如图,AC平分∠BAD,∠1=∠2,那么AB=AD成立吗?请说明理由.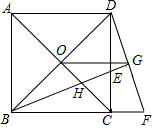 如图,点O是正方形ABCD的对角线交点,BE平分∠DBC,交DC于点E,交AC于H,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG,下列四个结论:①BG⊥DF;②OG∥AD;③BH=GH;④若正方形ABCD的边长是1,则CE=$\sqrt{2}$-1.其中正确的结论有①②④(把你认为正确结论的序号都填上).
如图,点O是正方形ABCD的对角线交点,BE平分∠DBC,交DC于点E,交AC于H,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG,下列四个结论:①BG⊥DF;②OG∥AD;③BH=GH;④若正方形ABCD的边长是1,则CE=$\sqrt{2}$-1.其中正确的结论有①②④(把你认为正确结论的序号都填上).