题目内容
10. 如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的( )
如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的( )| A. | 三边中线的交点 | B. | 三条角平分线的交点 | ||
| C. | 三边高的交点 | D. | 三边垂直平分线的交点 |
分析 根据题意得:支撑点应是三角形的重心.根据三角形的重心是三角形三边中线的交点.
解答 解:∵支撑点应是三角形的重心,
∴三角形的重心是三角形三边中线的交点,
故选:A.
点评 考查了三角形的重心的概念和性质.注意数学知识在实际生活中的运用.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
18.用每分可抽30t水的抽水机来抽污水管道内的污水,估计积存的污水超过1200t而不足1500t,则将污水抽完所用时间x的取值范围是( )
| A. | 40<x≤50 | B. | 40≤x<50 | C. | 40<x<50 | D. | 40≤x≤50 |
15.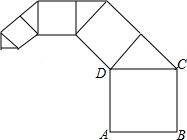 如图,正方形ABCD的边长为1,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…,按照此规律继续下去,则S2017的值为( )
如图,正方形ABCD的边长为1,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…,按照此规律继续下去,则S2017的值为( )
 如图,正方形ABCD的边长为1,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…,按照此规律继续下去,则S2017的值为( )
如图,正方形ABCD的边长为1,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…,按照此规律继续下去,则S2017的值为( )| A. | $\frac{1}{{2}^{2014}}$ | B. | $\frac{1}{{2}^{2015}}$ | C. | $\frac{1}{{2}^{2016}}$ | D. | $\frac{1}{{2}^{2017}}$ |
2.下列各式:①a;②$\frac{{-4x{y^2}}}{3}$;③x2-$\frac{1}{x}$+1;④0;⑤3+4y;⑥-$\frac{{2({x-y})}}{3}$中,其中是多项式的有( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
20.一种商品按销售量分三部分制定销售单价,如表:
(1)若买100件花250元,买300件花690元;买350件花790元;
(2)小明买这种商品花了338元,列方程求购买这种商品多少件?
(3)若小明花了n元(n>250),恰好购买0.45n件这种商品,求n的值.
| 销售量 | 单价 |
| 不超过100件的部分 | 2.5元/件 |
| 超过100件不超过300件的部分 | 2.2元/件 |
| 超过300件的部分 | 2元/件 |
(2)小明买这种商品花了338元,列方程求购买这种商品多少件?
(3)若小明花了n元(n>250),恰好购买0.45n件这种商品,求n的值.
 用4块相同的立方体搭成的几何体的主视图如图所示.
用4块相同的立方体搭成的几何体的主视图如图所示. 如图,AC平分∠BAD,∠1=∠2,那么AB=AD成立吗?请说明理由.
如图,AC平分∠BAD,∠1=∠2,那么AB=AD成立吗?请说明理由.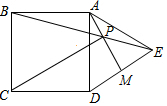 如图,正方形ABCD,点E为正方形外一点,△ADE为等边三角形,连BE,AM⊥DE交BE于P点,连CP.
如图,正方形ABCD,点E为正方形外一点,△ADE为等边三角形,连BE,AM⊥DE交BE于P点,连CP.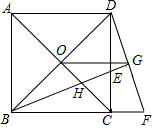 如图,点O是正方形ABCD的对角线交点,BE平分∠DBC,交DC于点E,交AC于H,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG,下列四个结论:①BG⊥DF;②OG∥AD;③BH=GH;④若正方形ABCD的边长是1,则CE=$\sqrt{2}$-1.其中正确的结论有①②④(把你认为正确结论的序号都填上).
如图,点O是正方形ABCD的对角线交点,BE平分∠DBC,交DC于点E,交AC于H,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG,下列四个结论:①BG⊥DF;②OG∥AD;③BH=GH;④若正方形ABCD的边长是1,则CE=$\sqrt{2}$-1.其中正确的结论有①②④(把你认为正确结论的序号都填上).