题目内容
19. 如图,在△ABC中,点D、E、F分别是AB、AC、BC的中点,现以线段AC,BC为斜边向△ABC的外侧作直角三角形,分别是△APC、△BQC,且DP=DQ
如图,在△ABC中,点D、E、F分别是AB、AC、BC的中点,现以线段AC,BC为斜边向△ABC的外侧作直角三角形,分别是△APC、△BQC,且DP=DQ(1)求证:△PED≌△DFQ;
(2)求证:CA•CQ=CB•CP.
分析 (1)由三角形中位线定理和直角三角形斜边上的中线性质可以得出PE=DF,DE=QF,由SSS证明△PED≌△DFQ即可;
(2)证出∠ACP=∠BCQ,证明△APC∽△BQC,得出对应边成比例$\frac{CA}{CB}=\frac{CP}{CQ}$,即可得出结论.
解答 (1)证明:∵点D、E、F分别是AB、AC、BC的中点,∠APC=∠BQC=90°,
∴DF=$\frac{1}{2}$AC,DF∥AC,DE=$\frac{1}{2}$BC,DE∥BC,PE=$\frac{1}{2}$AC,QF=$\frac{1}{2}$BC,
∴PE=DF,DE=QF,
在△PED和△DFQ中,$\left\{\begin{array}{l}{DP=DQ}&{\;}\\{PE=DF}&{\;}\\{DE=QF}&{\;}\end{array}\right.$,
∴△PED≌△DFQ(SSS);
(2)证明:∵DE∥BC,DF∥AC,
∴∠AED=∠ECF,∠BFD=∠ECF,
∴∠AED=∠BFD,
∵△PED≌△DFQ,
∴∠PED=∠DFQ,
∴∠AEP=∠BFQ,
∵PE=$\frac{1}{2}$AC=CE,QF=$\frac{1}{2}$BC=CF,
∴∠EPC=∠ECP=$\frac{1}{2}$∠AEP,∠FCQ=∠FQC=$\frac{1}{2}$∠BFQ,
∴∠ACP=∠BCQ,
又∵∠APC=∠BQC=90°,
∴△APC∽△BQC,
∴$\frac{CA}{CB}=\frac{CP}{CQ}$,
∴CA•CQ=CB•CP.
点评 本题考查了相似三角形的判定与性质、全等三角形的判定与性质、三角形中位线定理、直角三角形斜边上的中线性质;熟练掌握三角形中位线定理和直角三角形的性质,证明三角形全等和三角形相似是解决问题的关键.

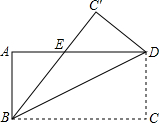 如图,矩形ABCD沿着直线BD折叠,使点C落在C'处,BC'交AD于点E,已知AD=8,AB=4,求△BED的面积.
如图,矩形ABCD沿着直线BD折叠,使点C落在C'处,BC'交AD于点E,已知AD=8,AB=4,求△BED的面积. 如图,电力公司为鼓励市民节约用电,采取按月用电量分段收费办法,若某户居民每月应交电费y(元)与用电量x(千瓦时)的函数图象是一条折线,根据图象解下列问题:
如图,电力公司为鼓励市民节约用电,采取按月用电量分段收费办法,若某户居民每月应交电费y(元)与用电量x(千瓦时)的函数图象是一条折线,根据图象解下列问题: 如图,在正方形ABCD的边BC的延长线上取一点E,使CE=CA,连接AE交CD于F,(1)求∠AFD的度数;(2)当BC=4cm时,求△ACE的面积.
如图,在正方形ABCD的边BC的延长线上取一点E,使CE=CA,连接AE交CD于F,(1)求∠AFD的度数;(2)当BC=4cm时,求△ACE的面积.
 如图,∠BAD=90°,射线AC平分∠BAE.
如图,∠BAD=90°,射线AC平分∠BAE.