题目内容
14.解方程:$\frac{{x}^{2}-3}{x}$+$\frac{3x}{{x}^{2}-3}$=$\frac{13}{2}$.分析 首先用换元法把原方程化为y+$\frac{3}{y}$=$\frac{13}{2}$,再用去分母法求出y的值,然后代入求出x的值,再检验即可.
解答 解:设$\frac{{x}^{2}-3}{x}$=y,则原方程化为y+$\frac{3}{y}$=$\frac{13}{2}$,
方程两边同乘以2y得:2y2+6=13y,
解得:y=$\frac{1}{2}$或y=6,
当y=$\frac{1}{2}$时,$\frac{{x}^{2}-3}{x}$=$\frac{1}{2}$,
解得:x=-1.5,或x=2,
经检验,x=-1.5,x=2是原方程的解;
当y=6时,$\frac{{x}^{2}-3}{x}$=6,
解得:x=3±2$\sqrt{3}$,
经检验,x=3±2$\sqrt{3}$是原方程的解;
因此,原方程的解为x1=-1.5,x2=2,x3=3$+2\sqrt{3}$,x4=3-2$\sqrt{3}$.
点评 本题主要考查解分式方程的解法以及换元法的应用;关键在于“转化思想”,把分式方程转化为整式方程求解,最后一定注意要验根.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
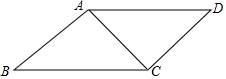 如图,在?ABCD中,AB=4cm,AC=6cm,∠BAC=90°,则BD之长为10cm.
如图,在?ABCD中,AB=4cm,AC=6cm,∠BAC=90°,则BD之长为10cm.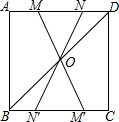 如图,在正方形ABCD中,连接BD,点O是BD的中点,若点M、N是边AD上的两点,连接MO,NO,并分别延长与边BC相交于点M′,N′.
如图,在正方形ABCD中,连接BD,点O是BD的中点,若点M、N是边AD上的两点,连接MO,NO,并分别延长与边BC相交于点M′,N′. 如图,在△ABC中,点D、E、F分别是AB、AC、BC的中点,现以线段AC,BC为斜边向△ABC的外侧作直角三角形,分别是△APC、△BQC,且DP=DQ
如图,在△ABC中,点D、E、F分别是AB、AC、BC的中点,现以线段AC,BC为斜边向△ABC的外侧作直角三角形,分别是△APC、△BQC,且DP=DQ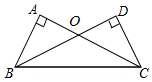 如图,∠A=∠D=90°,添加下列一个条件:①AB=CD;②AC=BD;③OB=OC;④∠ABC=∠BCD,其中能使△ABC≌△DCB成立的有( )
如图,∠A=∠D=90°,添加下列一个条件:①AB=CD;②AC=BD;③OB=OC;④∠ABC=∠BCD,其中能使△ABC≌△DCB成立的有( )