题目内容
4. 如图,在正方形ABCD的边BC的延长线上取一点E,使CE=CA,连接AE交CD于F,(1)求∠AFD的度数;(2)当BC=4cm时,求△ACE的面积.
如图,在正方形ABCD的边BC的延长线上取一点E,使CE=CA,连接AE交CD于F,(1)求∠AFD的度数;(2)当BC=4cm时,求△ACE的面积.
分析 (1)根据∠AFD=∠CAF+∠ACD,只要求出∠CAF,∠ACF的度数即可.
(2)根据S△ACE=$\frac{1}{2}$•CE•AB,求出CE即可.
解答  解:∵四边形ABCD是正方形,
解:∵四边形ABCD是正方形,
∴∠ACB=∠ACF=45°,
∵CA=CE,
∴∠CAE=∠E,
∵∠CAE+∠E=∠ACB=45°,
∴∠CAE=22.5°,
∴∠AFD=∠CAF+∠ACD=22.5°+45°=67.5°.
(2)在Rt△ABC中,AC=CE=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,
∴S△ACE=$\frac{1}{2}$•CE•AB=$\frac{1}{2}$×4$\sqrt{2}$×4=8$\sqrt{2}$.
点评 本题考查正方形的性质、等腰三角形的性质、三角形的外角的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在△ABC中,点D、E、F分别是AB、AC、BC的中点,现以线段AC,BC为斜边向△ABC的外侧作直角三角形,分别是△APC、△BQC,且DP=DQ
如图,在△ABC中,点D、E、F分别是AB、AC、BC的中点,现以线段AC,BC为斜边向△ABC的外侧作直角三角形,分别是△APC、△BQC,且DP=DQ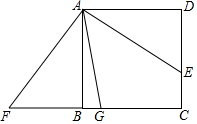 如图,E是正方形ABCD上一点,△ABF由△ADE旋转所得
如图,E是正方形ABCD上一点,△ABF由△ADE旋转所得