题目内容
11.已知,如图(1),PB为⊙O的割线,直线PC与⊙O有公共点C,且PC2=PA×PB,(1)求证:①∠PCA=∠PBC;②直线PC是⊙O的切线;
(2)如图(2),作弦CD,使CD⊥AB,连接AD、BC,若AD=2,BC=6,求⊙O的半径.
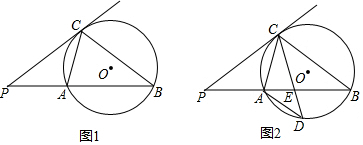
分析 (1)?根据已知条件得到$\frac{PA}{PC}=\frac{PC}{PB}$,推出△PCA∽△PBC,根据相似三角形的性质得到∠PCA=∠PBC,作直径CF,连接AF,则∠CAF=90°,得到∠PCA+∠FCA=90°,P过直径的一端点C,于是得到结论;
?(2)作直径BE,连接CE、AE.则∠BCE=∠BAE=90°,推出AE∥CD,得到$\widehat{AD}=\widehat{CE}$,根据勾股定理得到BE=2$\sqrt{10}$,即可得出结果.
解答 (1)?证明:∵PC2=PA×PB,
∴$\frac{PA}{PC}=\frac{PC}{PB}$,
∵∠CPA=∠BPC,
∴△PCA∽△PBC,
∴∠PCA=∠PBC,
作直径CF,连接AF,则∠CAF=90°,
∴∠F+∠FCA=90°,
∵∠F=∠B,∠PCA=∠PBC,
∴∠PCA+∠FCA=90°,
∵PC经过直径的一端点C,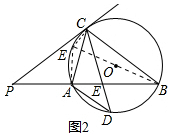
∴直线PC是⊙O的切线;
?(2)解:作直径BE,连接CE、AE.则∠BCE=∠BAE=90°,
∵CD⊥AB,
∴AE∥CD,
∴$\widehat{AD}=\widehat{CE}$,
∴AD=CE=2,
∵BC=6,
∴在Rt△BCE中,由勾股定理得:
BE2=CE2+BC2=22+62=40,
∴BE=2$\sqrt{10}$,
∴⊙O的半径为$\sqrt{10}$.
点评 本题考查了相似三角形的判定和性质,切线的判定,圆周角定理,勾股定理,正确的作出辅助线是解题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
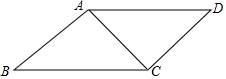 如图,在?ABCD中,AB=4cm,AC=6cm,∠BAC=90°,则BD之长为10cm.
如图,在?ABCD中,AB=4cm,AC=6cm,∠BAC=90°,则BD之长为10cm. 如图,在△ABC中,点D、E、F分别是AB、AC、BC的中点,现以线段AC,BC为斜边向△ABC的外侧作直角三角形,分别是△APC、△BQC,且DP=DQ
如图,在△ABC中,点D、E、F分别是AB、AC、BC的中点,现以线段AC,BC为斜边向△ABC的外侧作直角三角形,分别是△APC、△BQC,且DP=DQ
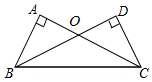 如图,∠A=∠D=90°,添加下列一个条件:①AB=CD;②AC=BD;③OB=OC;④∠ABC=∠BCD,其中能使△ABC≌△DCB成立的有( )
如图,∠A=∠D=90°,添加下列一个条件:①AB=CD;②AC=BD;③OB=OC;④∠ABC=∠BCD,其中能使△ABC≌△DCB成立的有( ) 如图中,正方形ABCD的面积是64m2,DC与EC的长度比是5:3,求三角形CDE的面积.(用比例解)
如图中,正方形ABCD的面积是64m2,DC与EC的长度比是5:3,求三角形CDE的面积.(用比例解)