Question

9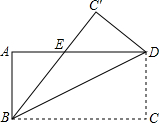．如图，矩形ABCD沿着直线BD折叠，使点C落在C'处，BC'交AD于点E，已知AD=8，AB=4，求△BED的面积．

Answer 1

分析 S_△BED=$\frac{1}{2}$DE•AB，所以需求DE的长．根据∠C′BD=∠DBC=∠BDA得DE=BE，设DE=x，则AE=8-x．根据勾股定理求BE即DE的长．

解答 解：∵AD∥BC（矩形的性质），
∴∠DBC=∠BDA（两直线平行，内错角相等）；
∵∠C′BD=∠DBC（翻折的性质），
∴∠C′BD=∠BDA（等量代换），
∴DE=BE（等角对等边）；
设DE=x，则AE=8-x．
在Rt△ABE中，x²=4²+（8-x）²．
解得x=5．
∴S_△DBE=$\frac{1}{2}$×5×4=10．

点评 此题通过折叠变换考查了三角形的有关知识，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后对应边、角相等．