题目内容
10. 按照题意,画出图形,并计算:
按照题意,画出图形,并计算:(1)如图,点A、O、B在同一条直线上,画射线OD、OC、OE,使射线OD和射线OE分别平分∠AOC和∠BOC.(∠AOC和∠BOC都小于180°);
(2)根据(1)中条件,若∠BOD=116°,求∠BOE的大小.
分析 (1)依照题意,画出图形即可;
(2)(方法一)根据角平分线的定义可得出∠AOD=∠COD=$\frac{1}{2}$∠AOC、∠COE=∠BOE=$\frac{1}{2}$∠BOC,根据邻补角互补结合∠BOD=116°可得出∠AOD的度数,进而可得出∠AOC、∠BOC的度数,再根据角平分线的定义即可得出∠BOE的度数;
(方法二)根据角平分线的定义结合邻补角互补可得出∠DOE=90°,将其代入∠BOE=∠BOD-∠DOE中可求出∠BOE的度数.
解答 解:(1)依照题意,画出图形.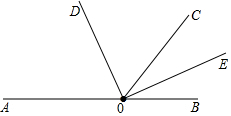
(2)(方法一)∵射线OD和射线OE分别平分∠AOC和∠BOC,
∴∠AOD=∠COD=$\frac{1}{2}$∠AOC,∠COE=∠BOE=$\frac{1}{2}$∠BOC.
∵∠BOD=116°,
∴∠AOD=180°-∠BOD=64°,
∴∠AOC=2∠AOD=128°.
∵∠AOC+∠BOC=180°,
∴∠BOC=52°,
∴∠BOE=$\frac{1}{2}$∠BOC=26°.
(方法二)∵射线OD和射线OE分别平分∠AOC和∠BOC,
∴∠AOD=∠COD=$\frac{1}{2}$∠AOC,∠COE=∠BOE=$\frac{1}{2}$∠BOC.
∵∠AOC+∠BOC=180°,
∴∠DOE=$\frac{1}{2}$(∠AOC+∠BOC)=90°,
∴∠BOE=∠BOD-∠DOE=26°.
点评 本题考查了角平分线的定义、邻补角以及角的计算,解题的关键是:(1)依照题意画出图形;(2)(方法一)根据角平分线的定义利用角的计算找出∠AOC、∠BOC的度数;(方法二)根据角平分线的定义结合邻补角互补找出∠DOE=90°.

练习册系列答案
相关题目
15. 为了解某校七年级学生的身高情况,随机抽取该校男生、女生进行抽样调查,已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:
为了解某校七年级学生的身高情况,随机抽取该校男生、女生进行抽样调查,已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:
身高情况分组表(单位:cm)
根据图表提供的信息,回答下列问题:
(1)样本中,男生人数为40人,男生身高类别C的组中值为162.5,男生身高类别B的频率为0.3;
(2)样本中,女生身高在E组的人数为2人,女生类别D的频数所对应的扇形圆心角为54°;
(3)已知该校共有男生400人,女生380人,请估计身高在160≤x<170之间的学生约有多少人?
 为了解某校七年级学生的身高情况,随机抽取该校男生、女生进行抽样调查,已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:
为了解某校七年级学生的身高情况,随机抽取该校男生、女生进行抽样调查,已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:身高情况分组表(单位:cm)
| 组别 | 身高 |
| A | 145≤x<155 |
| B | 155≤x<160 |
| C | 160≤x<165 |
| D | 165≤x<170 |
| E | 170≤x<175 |
(1)样本中,男生人数为40人,男生身高类别C的组中值为162.5,男生身高类别B的频率为0.3;
(2)样本中,女生身高在E组的人数为2人,女生类别D的频数所对应的扇形圆心角为54°;
(3)已知该校共有男生400人,女生380人,请估计身高在160≤x<170之间的学生约有多少人?
 如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=14°,求∠AOC的度数.
如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=14°,求∠AOC的度数. 如图,∠BOC在∠AOB的外部,∠AOC与∠BOC互为补角,OD平分∠AOC,∠BOD:∠BOC=3:4,求∠BOD的度数.
如图,∠BOC在∠AOB的外部,∠AOC与∠BOC互为补角,OD平分∠AOC,∠BOD:∠BOC=3:4,求∠BOD的度数.