题目内容
18. 在△ABC中,BC=4,AB=5,AC=3,CD⊥AB于D,求CD的长.
在△ABC中,BC=4,AB=5,AC=3,CD⊥AB于D,求CD的长.
分析 利用勾股定理逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形可得△ABC是直角三角形,再根据三角形面积公式可求CD的长.
解答 解:∵在△ABC中,BC=4,AB=5,AC=3,
又∵42+32=52,
即BC2+AC2=AB2,
∴△ABC是直角三角形,
则$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CD,即$\frac{1}{2}$×3×4=$\frac{1}{2}$×5•CD,
解得CD=2.4.
故CD的长是2.4.
点评 此题主要考查了勾股定理逆定理和三角形面积,关键是掌握勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.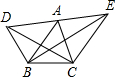 如图,已知A是DE的中点,设△DBC,△ABC,△EBC的面积分别为S1,S2,S3,则S1,S2,S3的关系为( )
如图,已知A是DE的中点,设△DBC,△ABC,△EBC的面积分别为S1,S2,S3,则S1,S2,S3的关系为( )
 如图,已知A是DE的中点,设△DBC,△ABC,△EBC的面积分别为S1,S2,S3,则S1,S2,S3的关系为( )
如图,已知A是DE的中点,设△DBC,△ABC,△EBC的面积分别为S1,S2,S3,则S1,S2,S3的关系为( )| A. | ${S_2}=\frac{3}{2}({S_1}+{S_3})$ | B. | ${S_2}=\frac{1}{2}({S_3}-{S_1})$ | C. | ${S_2}=\frac{1}{2}({S_1}+{S_3})$ | D. | ${S_2}=\frac{3}{2}({S_3}-{S_1})$ |
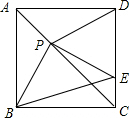 如图,正方形ABCD中,对角线AC上有一点P,连接BP、DP,过点P作PE⊥PB交CD于点E,连接BE.
如图,正方形ABCD中,对角线AC上有一点P,连接BP、DP,过点P作PE⊥PB交CD于点E,连接BE.