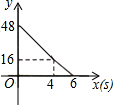题目内容
14.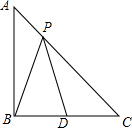 已知:如图,在等腰Rt△ABC中,∠ABC=90°,AB=2,D为BC的中点,P为线段AC上任意一点,则PB+PD的最小值为$\sqrt{5}$.
已知:如图,在等腰Rt△ABC中,∠ABC=90°,AB=2,D为BC的中点,P为线段AC上任意一点,则PB+PD的最小值为$\sqrt{5}$.
分析 首先确定DC′=DP+PC′=DP+BP的值最小,然后根据勾股定理计算.
解答 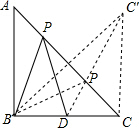 解:作点B关于直线AC的对称点C′,连接DC′,交AC于P,连接BP,
解:作点B关于直线AC的对称点C′,连接DC′,交AC于P,连接BP,
此时DP+BP=DP+PC′=DC′的值最小.
∵D为BC的中点,∴BD=1,DC=1,
∴BC=AB=2,
连接CC′,由对称性可知∠C′BC=∠BC′C=45°,
∴∠BCC′=90°,
∴CC′⊥BC,∠CBC′=∠BC′C=45°,
∴BC=CC′=2,
根据勾股定理可得DC′=$\sqrt{CC{′}^{2}+C{D}^{2}}$=$\sqrt{5}$.
故答案为:$\sqrt{5}$.
点评 此题考查了线路最短的问题,确定动点E何位置时,使PB+PD的值最小是关键.

练习册系列答案
相关题目
19.如果菱形的边长是α,一个内角是60度,那么菱形较短的对角线长等于( )
| A. | $\frac{1}{2}α$ | B. | $\frac{{\sqrt{3}}}{2}a$ | C. | a | D. | $\sqrt{3a}$ |
6.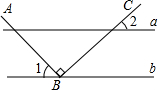 如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,则∠2的度数为( )
如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,则∠2的度数为( )
 如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,则∠2的度数为( )
如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,则∠2的度数为( )| A. | 35° | B. | 45° | C. | 55° | D. | 125° |
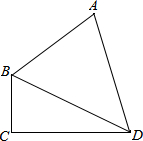 如图,四边形ABCD中,已知AB=10,CD=12,对角线BD平分∠ABC,∠ADB=45°,∠BCD=90°,则边BC的长度为4或6.
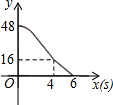
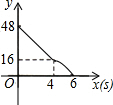
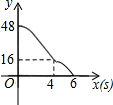
如图,四边形ABCD中,已知AB=10,CD=12,对角线BD平分∠ABC,∠ADB=45°,∠BCD=90°,则边BC的长度为4或6.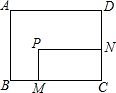 如图,矩形ABCD,AB=6,AD=8;动点M、N从点C出发,分别沿CB、CD以每秒2个单位长度和每秒1个单位长度的速度运动,分别至点B、点D停止.作矩形PMCN.若运动时间为x(单位:s),设矩形ABCD除去矩形PMCN后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是( )
如图,矩形ABCD,AB=6,AD=8;动点M、N从点C出发,分别沿CB、CD以每秒2个单位长度和每秒1个单位长度的速度运动,分别至点B、点D停止.作矩形PMCN.若运动时间为x(单位:s),设矩形ABCD除去矩形PMCN后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是( )