题目内容
4.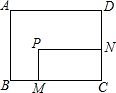 如图,矩形ABCD,AB=6,AD=8;动点M、N从点C出发,分别沿CB、CD以每秒2个单位长度和每秒1个单位长度的速度运动,分别至点B、点D停止.作矩形PMCN.若运动时间为x(单位:s),设矩形ABCD除去矩形PMCN后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是( )
如图,矩形ABCD,AB=6,AD=8;动点M、N从点C出发,分别沿CB、CD以每秒2个单位长度和每秒1个单位长度的速度运动,分别至点B、点D停止.作矩形PMCN.若运动时间为x(单位:s),设矩形ABCD除去矩形PMCN后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是( )| A. | 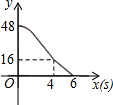 | B. | 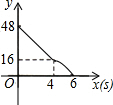 | C. | 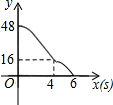 | D. | 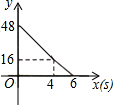 |
分析 根据题意知,剩余部分面积分两种情况:①点M在CB上运动、点N在CD运动时,即0≤x≤4;②点M到达终点B、点N在CD上运动时,即4<x≤6;根据以上两种情况分别用矩形ABCD的面积减去矩形PMCN的面积列出函数关系式可得答案.
解答 解:根据题意,CM=2x,CN=x
当0≤x≤4时,y=6×8-2x•x=-2x2+48,
此时y与x满足二次函数关系;
当4<x≤6时,y=6×8-8×x=-8x+48,
此时y与x满足一次函数关系;
故选:A.
点评 本题主要考查动点问题的函数图象,根据题意分类讨论是前提和基础,在两种前提下根据相等关系列出函数关系式是解题的关键.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
9.如果一个三角形的三边长为5、12、13,与其相似的三角形的最长的边长为39,那么较大的三角形的面积为( )
| A. | 90 | B. | 180 | C. | 270 | D. | 540 |
16.某校九(1)班进行了一次体育测试,期中第一小组的成绩分别是(单位:分)30,25,29,28,28,30,29,28,20,28,27,30.这组数据的众数和中位数分别是( )
| A. | 28分,28分 | B. | 30分,28分 | C. | 28分,27.5分 | D. | 30分,27.5分 |
13.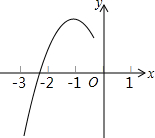 已知抛物线y=ax2+bx+c的顶点为D(-1,3),与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:
已知抛物线y=ax2+bx+c的顶点为D(-1,3),与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:
①b2-4ac>0;②c-a=3;③a+b+c<0;④方程ax2+bx+c=m(m≥2)一定有实数根,其中正确的结论为( )
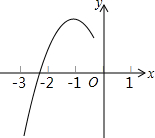 已知抛物线y=ax2+bx+c的顶点为D(-1,3),与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:
已知抛物线y=ax2+bx+c的顶点为D(-1,3),与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:①b2-4ac>0;②c-a=3;③a+b+c<0;④方程ax2+bx+c=m(m≥2)一定有实数根,其中正确的结论为( )
| A. | ②③ | B. | ①③ | C. | ①②③ | D. | ①②④ |
14.某水果店计划购进苹果和丑桔共140千克,这两种水果的进价、售价如表所示:
(1)若该水果店购进这两种水果的进货款为1000元,求水果店购进这两种水果各多少千克.
(2)若该水果店决定丑桔的进货量不超过苹果进货量的3倍,应怎样安排进货才能使水果店在销售完这批水果时获利最多?
| 进价(元/千克) | 售价(元/千克) | |
| 苹果 | 5 | 8 |
| 丑桔 | 9 | 13 |
(2)若该水果店决定丑桔的进货量不超过苹果进货量的3倍,应怎样安排进货才能使水果店在销售完这批水果时获利最多?
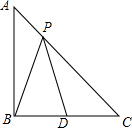 已知:如图,在等腰Rt△ABC中,∠ABC=90°,AB=2,D为BC的中点,P为线段AC上任意一点,则PB+PD的最小值为$\sqrt{5}$.
已知:如图,在等腰Rt△ABC中,∠ABC=90°,AB=2,D为BC的中点,P为线段AC上任意一点,则PB+PD的最小值为$\sqrt{5}$.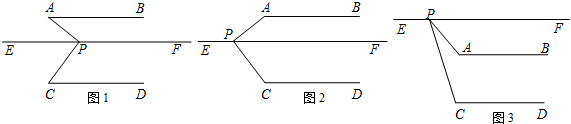
 如图,在Rt△ABC中,∠C=90°,AC=14,tanA=$\frac{3}{4}$,点D是边AC上一点,AD=8,点E是边AB上一点,以点E为圆心,EA为半径作圆,经过点D,点F是边AC上一动点(点F不与A、C重合),作FG⊥EF,交射线BC于点G.
如图,在Rt△ABC中,∠C=90°,AC=14,tanA=$\frac{3}{4}$,点D是边AC上一点,AD=8,点E是边AB上一点,以点E为圆心,EA为半径作圆,经过点D,点F是边AC上一动点(点F不与A、C重合),作FG⊥EF,交射线BC于点G.