题目内容
4.有五张正面分别标有数字-1,0,1,2,3的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中再取一张,将该卡片上的数字记为a,则a的值是不等式$\left\{\begin{array}{l}3x-1>-4\\ 2x+3<10\end{array}\right.$的解,又使关于x的一元二次方程(a-2)x2+x+2=0有实数根的概率是$\frac{2}{5}$.分析 首先求得关于x的不等式$\left\{\begin{array}{l}3x-1>-4\\ 2x+3<10\end{array}\right.$有实数解时,a的取值范围,再利用概率公式即可求得答案.
解答 解:$\left\{\begin{array}{l}3x-1>-4\\ 2x+3<10\end{array}\right.$解不等式得:-1<x<3.5,
因为a取整数,
所以a=0,1,2,3,
因为关于x的一元二次方程(a-2)x2+x+2=0有实数根,可得a$≤2\frac{1}{8}$,且a≠2,
所以a取的值为0,1两个,
所以概率是$\frac{2}{5}$,
故答案为:$\frac{2}{5}$.
点评 此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
15.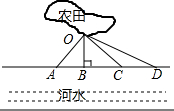 春节过后,某村计划挖一条水渠将不远处的河水引到农田(记作点O),以便对农田的小麦进行灌溉,现设计了四条路段OA,OB,OC,OD,如图所示,其中最短的一条路线是( )
春节过后,某村计划挖一条水渠将不远处的河水引到农田(记作点O),以便对农田的小麦进行灌溉,现设计了四条路段OA,OB,OC,OD,如图所示,其中最短的一条路线是( )
 春节过后,某村计划挖一条水渠将不远处的河水引到农田(记作点O),以便对农田的小麦进行灌溉,现设计了四条路段OA,OB,OC,OD,如图所示,其中最短的一条路线是( )
春节过后,某村计划挖一条水渠将不远处的河水引到农田(记作点O),以便对农田的小麦进行灌溉,现设计了四条路段OA,OB,OC,OD,如图所示,其中最短的一条路线是( )| A. | OA | B. | OB | C. | OC | D. | OD |
13.若4a2-2ka+9是一个完全平方的展开形式,则k的值为( )
| A. | 6 | B. | ±6 | C. | 12 | D. | ±12 |
 如图,将三角形ABC沿着DE折叠,使点A落在BC上的点F处,且DE∥BC,若∠B=70°,则∠BDF=40°.
如图,将三角形ABC沿着DE折叠,使点A落在BC上的点F处,且DE∥BC,若∠B=70°,则∠BDF=40°.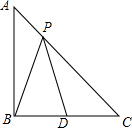 已知:如图,在等腰Rt△ABC中,∠ABC=90°,AB=2,D为BC的中点,P为线段AC上任意一点,则PB+PD的最小值为$\sqrt{5}$.
已知:如图,在等腰Rt△ABC中,∠ABC=90°,AB=2,D为BC的中点,P为线段AC上任意一点,则PB+PD的最小值为$\sqrt{5}$.