题目内容
2.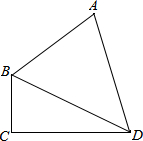 如图,四边形ABCD中,已知AB=10,CD=12,对角线BD平分∠ABC,∠ADB=45°,∠BCD=90°,则边BC的长度为4或6.
如图,四边形ABCD中,已知AB=10,CD=12,对角线BD平分∠ABC,∠ADB=45°,∠BCD=90°,则边BC的长度为4或6.
分析 如图,作辅助线;首先证明△FBD∽△GDA,进而得到DG•DF=BF•AG①;设BE=x,将①式中的线段分别用x来表示,得到关于x的方程,解方程即可解决问题.
解答 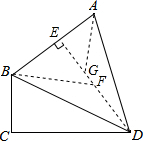 解:如图,过点D作DE⊥AB于点E;在ED上截取EF=EB,EG=EA;
解:如图,过点D作DE⊥AB于点E;在ED上截取EF=EB,EG=EA;
连接AG,BF;则∠BFE=∠AGE=45°,
∴∠BFD=∠DGA=135°;
∵BD平分∠ABC,且∠BCD=90°,
∴DE=DC=12,BE=BC;
∵∠FBD+∠BDF=∠BDF+∠ADG=45°,
∴∠FBD=∠GDA;
∴△FBD∽△GDA,
∴$\frac{BF}{DG}$=$\frac{DF}{AG}$,即DG•DF=BF•AG;
设BE=x,则DF=12-x,EG=EA=10-x;
BF=$\sqrt{2}$x,AG=$\sqrt{2}$EG=$\sqrt{2}$(10-x),
∴(x+2)(12-x)=$\sqrt{2}$(10-x)$\sqrt{2}$x,
整理得:x2-10x+24=0,
解得:x=4或6,
即边BC的长度为4或6.
故答案为:4或6.
点评 此题主要考查了相似三角形的判定及其性质的应用问题,解题的关键是作辅助线,构造相似三角形;灵活运用有关定理来分析、判断、解答是关键.

练习册系列答案
相关题目
13.若4a2-2ka+9是一个完全平方的展开形式,则k的值为( )
| A. | 6 | B. | ±6 | C. | 12 | D. | ±12 |
 如图,将三角形ABC沿着DE折叠,使点A落在BC上的点F处,且DE∥BC,若∠B=70°,则∠BDF=40°.
如图,将三角形ABC沿着DE折叠,使点A落在BC上的点F处,且DE∥BC,若∠B=70°,则∠BDF=40°. 如图,网格图中的每一格的边长都相等,列和行都用字母标记,按照先列后行的顺序,点O的位置可用(d,e)表示,则(c,d)可表示图中的点C.
如图,网格图中的每一格的边长都相等,列和行都用字母标记,按照先列后行的顺序,点O的位置可用(d,e)表示,则(c,d)可表示图中的点C.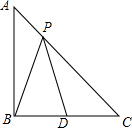 已知:如图,在等腰Rt△ABC中,∠ABC=90°,AB=2,D为BC的中点,P为线段AC上任意一点,则PB+PD的最小值为$\sqrt{5}$.
已知:如图,在等腰Rt△ABC中,∠ABC=90°,AB=2,D为BC的中点,P为线段AC上任意一点,则PB+PD的最小值为$\sqrt{5}$. 解不等式组:$\left\{\begin{array}{l}{2x>3x-2}\\{\frac{2x-1}{3}≥\frac{1}{2}x-\frac{2}{3}}\end{array}\right.$,并把解集在数轴上表示出来.
解不等式组:$\left\{\begin{array}{l}{2x>3x-2}\\{\frac{2x-1}{3}≥\frac{1}{2}x-\frac{2}{3}}\end{array}\right.$,并把解集在数轴上表示出来.