题目内容
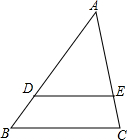 如图,
如图,| AB |
| AD |
| AC |
| AE |
| BC |
| DE |
| 6 |
| 5 |
考点:相似三角形的判定与性质
专题:
分析:利用相似三角形的判定定理直接判断两个三角形相似,利用相似三角形的周长比等于相似比,列出比例式求解即可解决问题.
解答:解:∵
=
=
=
,
∴△ABC∽△ADE;
设△ABC、△ADE的周长分别为x、y,由题意得:
,
解得x=24,y=20,
∴△ABC与△ADE的周长分别为24,20.
| AB |
| AD |
| AC |
| AE |
| BC |
| DE |
| 6 |
| 5 |
∴△ABC∽△ADE;
设△ABC、△ADE的周长分别为x、y,由题意得:
|
解得x=24,y=20,
∴△ABC与△ADE的周长分别为24,20.
点评:考查了相似三角形的判定及其性质的应用问题;解题的关键是灵活运用有关性质列出方程组来解题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
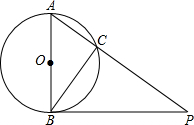 如图,已知AB是⊙O的直径,PB是⊙O的切线,PA交⊙O于C,AB=3cm,PB=4cm,则BC长为( )
如图,已知AB是⊙O的直径,PB是⊙O的切线,PA交⊙O于C,AB=3cm,PB=4cm,则BC长为( ) | A、5cm | B、2.4cm |
| C、3.6cm | D、1.8cm |
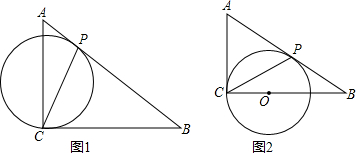
 如图,在直角梯形ABCD中,AD∥BC,∠BAD=90°,AB=4,CD=5,AD=6,动点P从点A开始以每秒1个单位长度的速度向点B匀速运动,动点Q从点B开始沿折线BC-CD以每秒2个单位长度的速度向点D匀速运动,过点P作PE⊥AB,交CD于点E,设点P、Q同时开始运动,且时间为t秒(t>0),当点P与点B重合时停止运动,点Q也随之停止运动.
如图,在直角梯形ABCD中,AD∥BC,∠BAD=90°,AB=4,CD=5,AD=6,动点P从点A开始以每秒1个单位长度的速度向点B匀速运动,动点Q从点B开始沿折线BC-CD以每秒2个单位长度的速度向点D匀速运动,过点P作PE⊥AB,交CD于点E,设点P、Q同时开始运动,且时间为t秒(t>0),当点P与点B重合时停止运动,点Q也随之停止运动.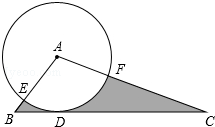 如图,在△ABC中,BC=6,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,∠EAF=120°,则图中阴影部分的面积是
如图,在△ABC中,BC=6,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,∠EAF=120°,则图中阴影部分的面积是 如图,在Rt△ABC中,CD是斜边AB上的中线,若CD=5,AC=6,则tan∠BCD的值是
如图,在Rt△ABC中,CD是斜边AB上的中线,若CD=5,AC=6,则tan∠BCD的值是